2章　what evolution is - 魚料理好きの日記

evolutionary dynamicsの基本概念replication,selection,mutationについて。
replication:自己の(遺伝情報も含めて)複製。
selection:異なる個体間での淘汰。
mutation:異なる（遺伝情報をもつ）個体の生産。

1.reproduction
期間毎にそのときの個体数x(t)とある正の定数rの積で増殖するとき、
$\dot{x}=rx$
と表され、解は
$x(t)=x_{0}e^{rt}$
となる。
これと同時に、ある正の定数dで死亡するとき、
$\dot{x}=(r-d)x$
と表され、寿命の平均は $\frac{1}{d}$ となり、個体の増加率はrとなる。
$\frac{r}{d}>1$ のときに、個体数は増加していく。

最大値Kの制限付き増加モデルは、上式に制限項をかけたもので
$\dot{x}=rx(1-\frac{x}{K})$
と表され、解は
$x(t)=\frac{Kx_{0}e^{rt}}{K+x_{0}(e^{rt}-1)}$
と表される。
この解はKに収束する。

今、K=1として差分方程式を考える。
$x_{t+1}=ax_{t}(1-x_{t})$
負の値を取らない条件は $0 \leq a \leq 4$ 。
収束値 $x^{\ast}$ はaの値によって変わる。
$0 \leq a <1$ のとき、 $x^{\ast}=0$ 。
[tex:1

f<-function(a,x){y<-a*x*(1-x)
                 return(y)}
t<-50
a<-1:40*0.1
x<-0.5
X<-matrix(0,t,length(a))
X[1,]<-x
for(i in 2:t){
X[i,]<-f(a,X[i-1,])
}
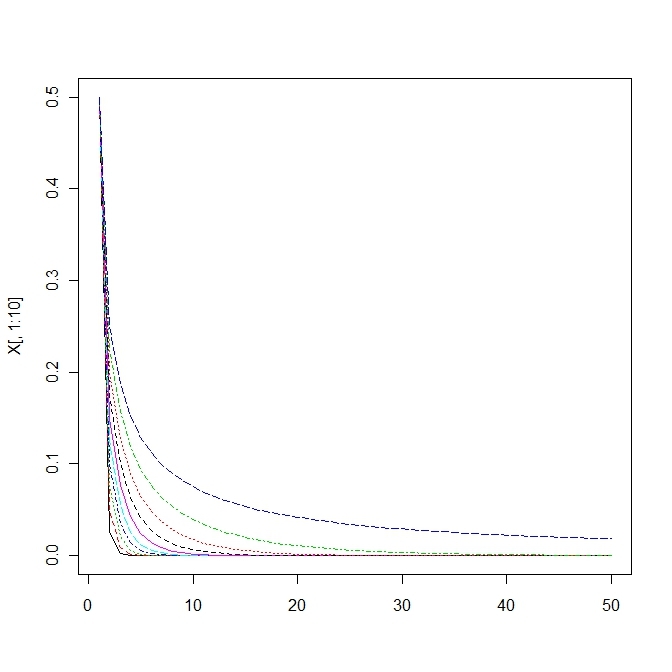
matplot(X[,1:10],type='l')
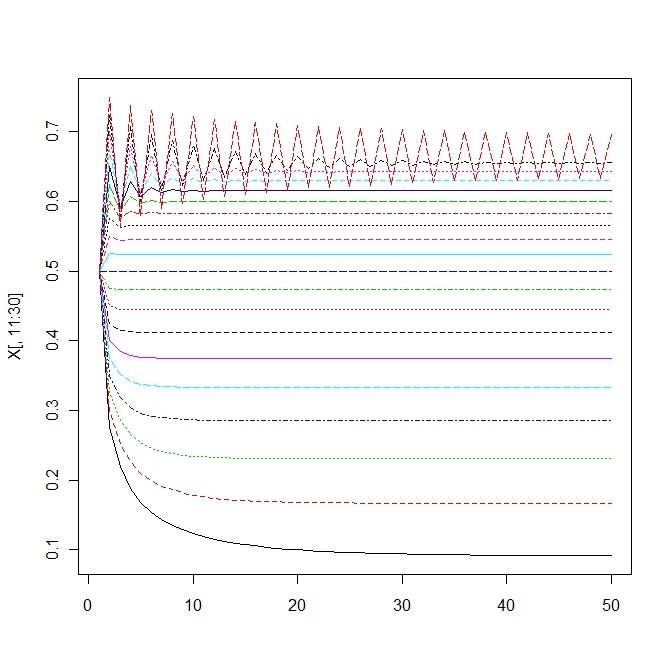
matplot(X[,11:30],type='l')
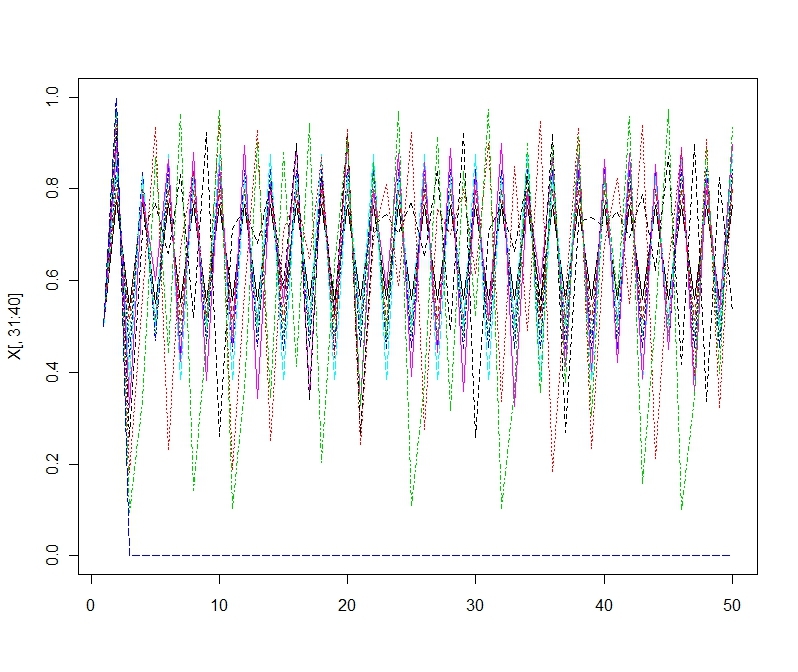
matplot(X[,31:40],type='l')

このモデルはさらに決定論的カオスで初期値鋭敏性をもつ。

f<-function(a,x){y<-a*x*(1-x)
                 return(y)}
t<-50
a<-4
x<-c(0.3156,0.3157)
X<-matrix(0,t,length(x))
X[1,]<-x
for(i in 2:t){
X[i,]<-f(a,X[i-1,])
}
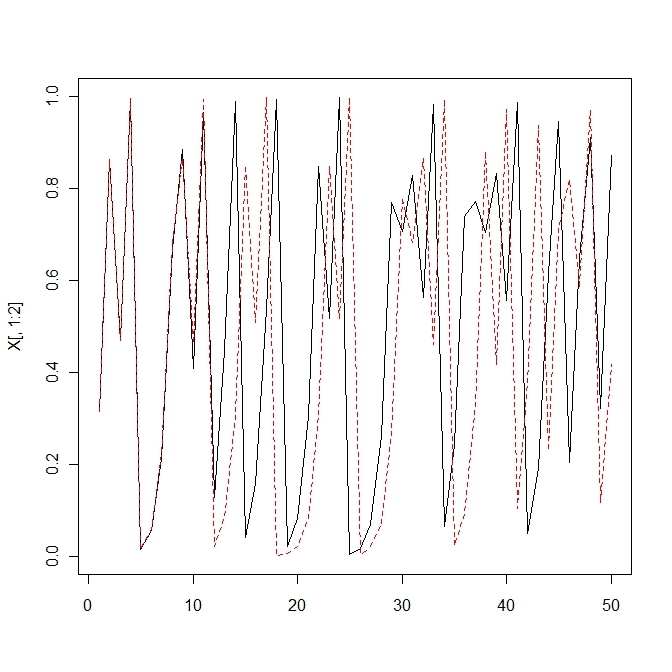
matplot(X[,1:2],type='l')

[:初期値0.3156と0.3157の挙動の違い]

2.selection
2種類の生物の個体数x(t),y(t)がそれぞれa,bの割合で初期値増殖するモデル
$\dot{x}=ax$ , $\dot{y}=by$
について
$\rho (t)=x(t)/y(t)$
とすることで、a,bの大きさで淘汰される側がわかる。

総個体数一定の条件x+y=1の下では
$\dot{x}=x(1-x)(a-b)$
が得られ、均衡は $x^{\ast}=0,1$ 。
また、a,bの大きさによって収束先が変わる。
これが適者生存の概念である。
多次元に応用すれば
$\phi = \sum{x_{i} f_{i}}$ かつ $\sum{x_{i}}=1$ として
$\dot{x_{i}}=x_{i}(f_{i}-\phi)$ とすると、
単体上で考えられる。
fが最も大きい個体に収束する。

a<-matrix(0,500,3)
a[1,1]<-runif(1)/2
a[1,2]<-runif(1)/2
a[1,3]<-1-a[1,1]-a[1,2]
f1<-1/2
f2<-1/3
f3<-1/6
S<-function(x,y,z){sigma<-sum(x*f1+y*f2+z*f3)
                    return(c(x+x*(f1-sigma),y+y*(f2-sigma),z+z*(f3-sigma)))}
for(i in 1:499){a[i+1,]<-S(a[i,1],a[i,2],a[i,3])}
library(rgl)
plot3d(a,type="l",col="2")

この３次元verでは初期状態(1/2,1/3,1/6)から(1,0,0)に収束する軌道になる。(f1が最も大きいので)

3.mutation
2タイプの個体X,Yの個体数x,yについてmutationを起こしてもう一方の個体を生む割合をそれぞれ $u_{1},u_{2}$ とすると
$\dot{x}=x(1-u_{1})+yu_{2}-\phi x$
$\dot{y}=x u_{1}+y(1-u_{2})-\phi y$
としてx,yの時間変化は表される。
$x+y=1$ とすると、 $\phi =1$ であり、
このときxの均衡値 $x^{\ast}=\frac{u_{2}}{u_{1}+u_{2}}$ となる。
3つ以上のタイプの場合、mutation matrix,Q= $[q_{ij}$ ]を用いて
$\dot{\vec{x}}=\vec{x}Q-\phi \vec{x}$ と表される。
Qはn*nの推移確率行列となる。

4.mating
閉鎖的な環境下、変異も起きない中でramdom matingが行われればallele頻度は保存される(Hardy-Weinbergの法則)