4章　Evolutionary games - 魚料理好きの日記

4.2 Nash equilibrium
２種類の生き物(もしくは戦略)A,Bがいて、AがそれぞれA,Bと出会った時の利得をa,bとし、Bの場合c,dとする。
これを↓のようなpayoff行列で表すとする。
$\matrix{ & A & B \cr A & a & b \cr B & c & d}$

このとき、
1.Aが狭義のNash均衡⇔a>c
2.AがNash均衡⇔a≧c
3.Bが狭義のNash均衡⇔d>b
4.BがNash均衡⇔d≧b

4.3 Evolutionary stable strategy(ESS)
Aが多数いる中で変異種Bがはびこらないような条件
AがESS⇔a>c or (a=c and b>d)

4.4 More than 2 strategies
strategy $S_{j}$ に対するstrategy $S_{i}$ のpayoffを $E(S_{i},S_{j})$ とする。

1.strategy $S_{k}$ が狭義のNash均衡⇔ $E(S_{k},S_{k})>E(S_{i},S_{k}), \forall i \neq k$
2.strategy $S_{k}$ がNash均衡⇔ $E(S_{k},S_{k}) \succeq E(S_{i},S_{k}), \forall i \neq k$
3.strategy $S_{k}$ がESS⇔ $E(S_{k},S_{k})>E(S_{i},S_{k}), \forall i \neq k$ もしくは $E(S_{k},S_{k})=E(S_{i},S_{k}), E(S_{k},S_{i})>E(S_{i},S_{i}), \forall i \neq k$
4.strategy $S_{k}$ が広義のESS⇔ $E(S_{k},S_{k})>E(S_{i},S_{k}), \forall i \neq k$ もしくは $E(S_{k},S_{k})=E(S_{i},S_{k}), E(S_{k},S_{i}) \succeq E(S_{i},S_{i}), \forall i \neq k$
条件の強さとして1>3>4>2

無敵なstrategyは $E(S_{k},S_{k})>E(S_{i},S_{k}),E(S_{k},S_{i})>E(S_{i},S_{i})$ で定義される

4.5 Replicator dynamics
戦略i(もしくは変異種)に対する戦略jのpayoffを $a_{ij}$ とするとn×nのpayoff行列Aができる。
また、fitnessを $f_{i}(\vec{x})=\sum^{n}_{j=1}a_{ij}x_{j}$ とすれば
再生産の方程式は $\dot{x_{i}}=x_{i}[ f_{i}-\phi]$ として表せる。

4.6 Hawk or Dove?
タカ派とハト派をモチーフにしたゲーム。
$\matrix{ & H & D \cr H & \frac{b-c}{2} & b \cr D & 0 & \frac{b}{2} }$
自分と敵のタカ派、ハト派をとる確率を $p_{1},p_{2}$ とすると
期待所得 $E(p_{1},p_{2})$ は $E(p_{1},p_{2})=\frac{b}{2}(1+p_{1}-p_{2}-\frac{c}{b}p_{1}p_{2})$ で表される。
安定点は $p^{\ast}=\frac{b}{c}$ のとき。

4.7 Thre is always a Nash equilibrium
自分も相手もn通りの戦略をとれるとし、それぞれの戦略をとる自分の分布を $\vec{p}=(p_{1},p_{2},...,p_{n})$ 、相手の分布を $\vec{q}=(q_{1},q_{2},...,q_{n})$ とする。
payoff matrixを $A={a_{ij}}$ とすれば、期待所得 $E(\vec{p},\vec{q})=\sum^{n}_{i=1}\sum^{n}_{j=1}a_{ij}p_{i}q_{j}=\vec{p}A\vec{q}$ と表せる。
このとき、 $\vec{p}A\vec{p}\geq\vec{q}A\vec{p} , \forall \vec{q}$ なる $\vec{p}$ が必ず存在する。
ペロン―フロベニウスの定理使えば証明できそう(たぶん)。

4.9 Game theory and ecology
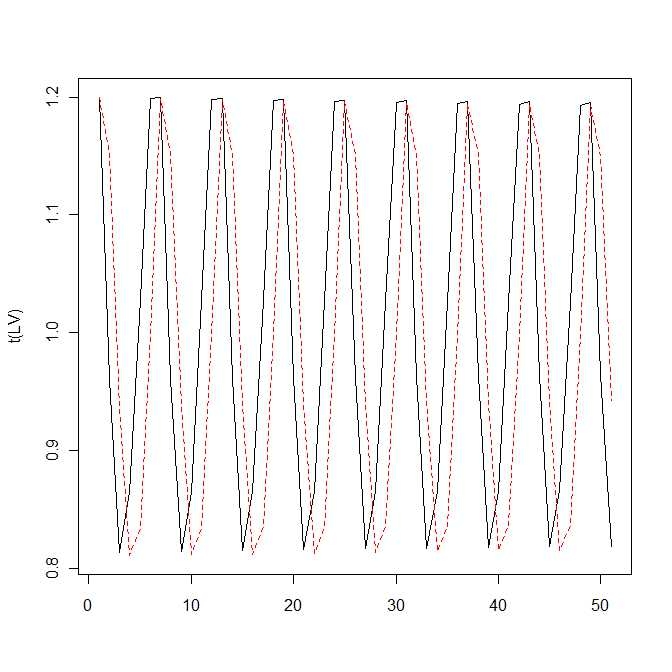
ロトカ・ヴォルテラの式について

a<-1
b<-1
c<-1
d<-1
f<-function(x,y){
x<-x+x*(a-b*y)
y<-y+y*(-c+d*x)
return(c(x,y))
}
n<-50
LV<-matrix(0,2,n+1)
LV[,1]<-c(1.2,1.2)
for(i in 1:n){
LV[,i+1]<-f(LV[1,i],LV[2,i])
}
matplot(t(LV),type="l")