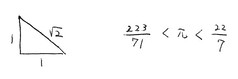数学と芸術にみる複素数の解釈 −その1−
先日、いつもご馳走目当てにお邪魔している (笑) 毎月の「例会」で、複素数や虚数の話が出ました。ゼロやマイナスの数を理解し当たり前のこととして受け入れるまでに、人間は数百年もの時間をかけ、現代は虚数の概念を受け入れつつある段階だというような話でした。ただし、小学生でも虚数を当たり前の感覚で受け入れられるようになるには、まだ100年や200年くらい掛かるのではないか、という部分で少し議論したのを覚えています。
ところが先日、朝日コムのサイトでサイエンスのページを見ていたら、右側のサイエンス関連雑誌の広告で、雑誌「ニュートン」の12月号がランキングの1位*1になっており、その特集が「虚数」じゃありませんか (ちょっと欲しいなぁ)。まったく、ユングの共時性なのかどうか分かりませんが、不思議な因果を感じました。
ユングの共時性は最近よく体験するので、そのこと自体興味はあるのですが、今回はその話はさておき、虚数についてちょっと考えてみたいと思ったわけです。
例会のお宅のご主人は画家でもあるのですが、数学や物理学にとても興味を持っていらっしゃり、知的好奇心いっぱいの素敵な方です。その時も、虚数とは、複素数とはということについていろいろ質問されたのですが、教科書的な通り一遍の解釈で説明してしまったように思います。
でも改めて考えてみると、虚数の定義やら複素数の数学的意味などを素人同士が議論しても、まだ一般的に浸透していないもののことですから、あまり意味がありません。もっと創造的で直感的な説明はできないものかとちょっと考えてみました。
ちなみに、物理学と天文学を大学で学んだとはいえ、数学は専門ではありません。でも、(嫌いだったので目もくれなかった) 化学の実験のクラスさえ取っていれば数学の学位ももらえるところまでいっていたので、まったくの門外漢でもありません。ちょうど、専門家と素人の間にいる、両方の見方を持った存在と (都合よく) 考えることにして、勝手な「数学と芸術にみる複素数の解釈」なんてものをここで展開してみることにしました。
さて、のっけから偉そうなことを書いてしまったのですが、果たして虚数をそんなに易しく解説することは可能なんでしょうか? 考えてみると、これは大変なことのように思えます。なので、あまり期待しないでくださいと、予めお断りしておきます (汗)。
で、ここでは「数学と芸術」を勝手に (!) 結びつけて説明しようと思うのですが、その前にまず、数の世界がどんなものであるかを、数の概念の歴史に照らして整理したいと思います。
(さらに、ここで展開する解釈は、かなり独自の見方であって、専門家による学術性を持ったものではないことを明記しておきます。あくまで、素人が思いついた解釈です。あしからず)
そしてもう1つ。説明に使う図はきったない手書きのものなので、とてもみすぼらしいですが、それはなにとぞご勘弁を。 (汗)
1)数とは何か
数とはなんでしょうか? 数や計算は、人間が考え出した便利な道具です。(映画「Matrix」に出てくるように) この宇宙が数字で成り立っているわけではなく、数という「概念」を人間が作り出し、それを使って様々な現象や状態を体現している、一種の「表現・表記」です。ここでは、その表現を、形を変えて眺めて見てみることにします。
まずは、数というもの自体、つまりは「数の世界」を1つの平面で現してみることにします。後述しますが、これはいわゆる「複素数平面」または「ガウス平面」と同じなので、この平面をガウス平面と呼ぶことにします。
その平面には、いままで人間が作り出してきたすべての数があると想像してみてください。
2)自然数
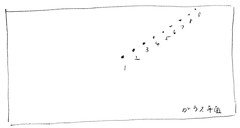
ガウス平面をよく見ると、平面上にいくつかの「点」が直線状に並んでいる様子が見えてきます。「1」、「2」、「3」・・・という、それぞれが一定の間隔で並んでいる点です。これは自然数と呼ばれるもので、人間が最初に物を数えるときに使いだした数字です。人が1人、2人とか、リンゴが1個、2個など、人間が作り出したというよりも、まさに「自然発生」した数字といえますが、その概念の認識は人間の文化的創造の結果です。
つまり、牛や豚のような家畜が何頭いるのかを数える場合、まだ (数そのものの概念ではなく) 数字を持っていなかった時代は、それと同数の木片や小石などを使って数を数えていたと思われます。特に初期の頃は、指を使っていたでしょう。この時点では、まだ自然数を「理解」するには至っていません。
そのうち頭のいい誰かが、地面や洞窟の壁に線を引き、記号を使って数える方法を編み出したのだと思われます。これで人間は自然数というものの概念を理解し、使えるようになったわけです。そしてここでは、それを『ガウス平面上に自然数の「点の並び」が浮き出る』と描写します。
ちなみに現在では、自然数を理解しているのは、何も人間だけではないと考えられています。動物の中にはいくつかの自然数を理解できるものもいます。例えばチンパンジーなどの霊長類はもとより、指で数えることができない (つまり頭の中で理解しているとしか考えられない) カラスなどの鳥類などでも、1や2という数の意味は分かるようです。特にカラスは、少なくとも3つまで数えられることがある実験で分かっています。
話がそれてしまいますが、気になるでしょうから、その実験のことを簡単に説明します。というか、実は実験ではなかったのですが。。。
昔、いたずらが過ぎるカラスが教会の鐘つき塔に巣をつくりました。そこで村人が追い払おうと銃を持って塔に上っていくと、カラスは人が塔にいる間は戻ってきません。そこで、二人が入り、一人だけ出て、カラスを騙そうとしたのですが、利口なカラスは一人と二人の違いに気づいて戻ってきません。結局、少しずつ人数を増やしていったところ、四人入って三人出てきてもダメでしたが、五人入って四人出てきたらカラスが戻ってきました。これでようやく、人間とカラスの知恵比べに決着が付きました。つまり、「1、2、3、いっぱい」というのがカラスの持つ数の世界というわけです。
3)分数
ガウス平面上には、まだ自然数の「点」が直線状に並んでいるだけですが、ある時人間は、1つのリンゴを2人で分けなければならない事態に直面しました。このとき、1人あたりのリンゴの数は2分の1になります。つまり、自然数で表現される大きさのものを、いくつかで分割するという考え方が理解されるようになります。紀元前2000年頃の古代エジプト時代には、土地の分割を行うために分数の表記がすでに使われていました。
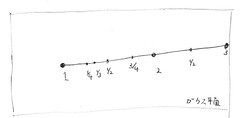
そして、これをガウス平面で考えると、平面上の点と点の間には何もないのではなく、そこにもいくつかの点が描けることになります。つまり、(ゼロではなく) 「1」を起点にした線分が描けます。
ちなみにこの頃になると、1次方程式の計算などが行われるようになり、「数学」という学問が確立されてきたといえます。
分数は正の整数を表記することもできるため、非常に便利な数です。しかし、すべての数を分数で表現できるわけではないことが徐々にわかってきます。例えば、古代ギリシャのピタゴラスの時代 (紀元前5世紀頃) には、2の平方根が分数で表記できないことを理解していたと言われています。
2の平方根以外にも、π や自然対数の底 e など、分数 (や後述の小数) で表現できない数が存在します。これらの数は無理数と呼ばれ、それに対応するものが有理数と呼ばれています。有理数とは、「2つの整数aとbを用いて a/b と表せる数」と定義されます。これに対し、無理数は、有理数でない「実数」と定義されます。
ただ、「実数」には、後述する負の数やゼロなども含まれるため、この時点ではまだ完全な数学的定義にはなっていません。しかし基本的な概念はすでに理解されていたと考えられます。
5)負の数
紀元前2世紀頃の中国では、負の数の概念が記されています。そして、インドやエジプトでも、1次方程式の解として負の数の存在が問題になってきます。例えば
4x + 20 = 0
という1次方程式の解は負の数になりますが、負の数を持つ方程式自体を馬鹿げたものだとして、負の数の存在はなかなか受け入れられませんでした。数学者でさえ、負の数についての規則を論じておきながら、その存在を否定する有様でした。
しかし8世紀頃に、イスラム地方で負の概念が理解されるようになります。ヨーロッパでは17世紀までなかなか浸透しませんでしたが、徐々に理解が進むようになりました。
この負の数は、ガウス平面においては、自然数の並びと反対側に一列にならぶ点として現すことができます。もちろん、理論上は負の数についても分数が論じられていたでしょうから、ここでは (ゼロでなく) 「−1」を起点にした線分を描くことができるようになります。
6)ゼロと実数
7世紀になり、負の数について理解が進んでいたインドでは、正の数と負の数の間にあるものとして、ゼロという概念が生まれました。正確には、今から1300〜1400年ほど前、インドの数学について書かれた書物に「ゼロ」が記述されていたことがわかっています。これにより、ゼロを含めた「整数」という概念が生まれました。
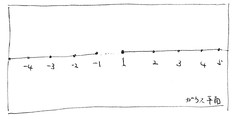
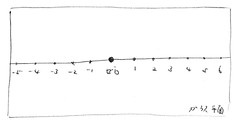
ただし、分数という概念がすでに理解されているので、整数だけでなく、整数の点と点の間の分割点、つまり分数も加えることで、点の連なりは線として表すことができます。つまり、ガウス平面上でいえば、負から正にかけて、ゼロを通る直線が描かれることになります。
a quickr pickr post
ちなみにキリストが生まれたのは紀元元年ですが、この時はまだゼロが発見されてなかったんですね。なので、紀元元年は紀元ゼロ年でなく、紀元1年です。紀元元年より前の年は、紀元前1年、紀元前2年、、、というように、やはり「1」から始まります。それで、世紀の最後の年は●100年になり、●●99年にならないようです。全知全能の神様の遣いとして降臨してきたキリスト様なんだから (違うかな?)、この時にちゃんと「ゼロ」というものを教えておいてくれれば、こんなややこしいことにはならなかったんですけどねー。これも試練なんでしょうか?
7)小数
小数の歴史はかなり浅いもので、1500年代に入ってベルギーのシモン・ステヴィンという人により考案されました。小数点を使った表記は、さらに数年〜数十年後になります。つまり、小数は発見されたのではなく「発明」された数学の小道具で、分数だと見づらい、計算するにの扱いにくい、などの理由で生まれたものです。
小数はとても便利なものですが、利便性を優先して作り出した表記なので、数学的な完璧さを備えていません。つまり、すべての分数を小数で表すことができないのです。このような小数を循環小数といいますが、これも単に表記上の問題であり、(個人的には) 数の理解というよりも道具の使い方といった感覚で捕らえるべきかと思われます。
虚数の歴史は、実は小数とほぼ同じです。二乗して「−1」になる数を i と表記し、このような数を虚数と呼びますが、i を表記する際に使われる根号記号 √ も、実はほぼ同じ頃に使われ始めたようです (最初の使用は1200年台とも言われていますが)。もちろん、前述したように平方根自体は古代ギリシャで登場していますので、ここで言っているのは根号「記号」のことです。こうしてみると、この時代は数学において革命的な時期だったのかも知れませんね。
ちなみに、レオナルド・ダ・ヴィンチが活躍し、コペルニクスが地動説を唱えたのも、この頃です。そして現在、虚数や複素数は高校で教わる内容になっていますが、とても一般的に理解が進み、「ゼロ」や「分数」のような市民権を得ているとは言いがたいものです。
まあ、歴史の長さからすれば仕方ないものですが、それでは「ゼロ」や「分数」のように、小学生でも「虚数」や「複素数」が当たり前のように理解される時代は、あと数百年後にくるのでしょうか?
もしその時代がくるなら、虚数と複素数について、もう少し直感的で興味が持てるような説明や解説が必要ではないかと思います。しかし、現在の高校の教科書でどのように教えているのか分かりませんが、とてもそのような教え方はしてないだろうと想像できます。たぶん、恐ろしく退屈で「定義」だけを暗記させるやり方ではないでしょうか。
そこで、という訳ではないですが、「数学と芸術にみる複素数の解釈 −その2−」では、単にそっけない定義ではなく、複素数の意味や意義、有用性、そして必要性について考えてみたいと思います。
(つづく)
*1:注意:11月下旬の時点です。今日 (日本時間の8日) は6位になってます