ラウスの定理から

久々の更新。メモ程度だけど。

入試問題とかで有名な話。
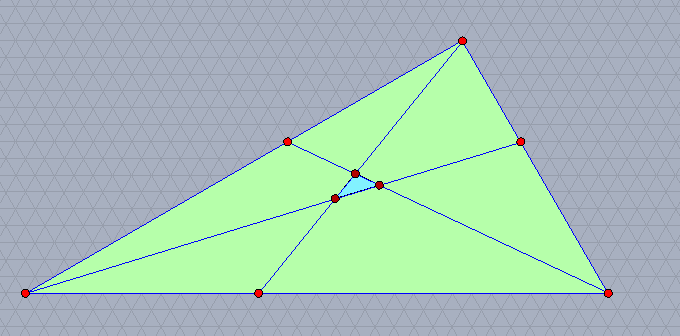
三角形の各辺の三等分点と，それぞれに向かい合う頂点を，向きを揃えて結ぶと，もとの三角形の1/7の面積の三角形ができる。

これはラウスの定理の一例になっている。
http://en.wikipedia.org/wiki/Routh's_theorem

三等分点は各辺に対して二つあるけど，向きを揃えて結べば，もとの三角形の1/7の面積の三角形ができるのは同じ。これは当たり前。

五等分点にすると，小三角形の面積は３倍になる。
三角形の各辺の五等分点（頂点に近い方）と，それぞれに向かい合う頂点を，向きを揃えて結ぶと，もとの三角形の3/7の面積の三角形ができる。

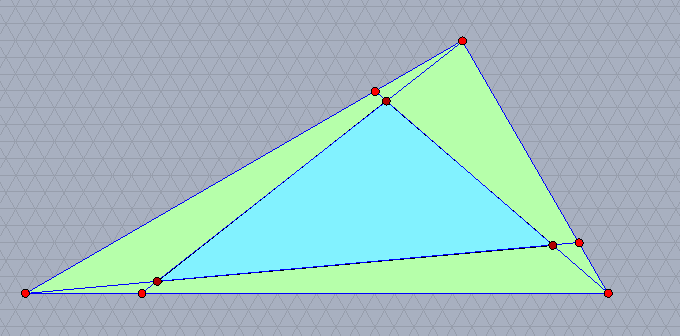
五等分点には，頂点から遠いものもある。
三角形の各辺の五等分点（頂点から遠いもの）と，それぞれに向かい合う頂点を，向きを揃えて結ぶと，もとの三角形の1/19の面積の三角形ができる。

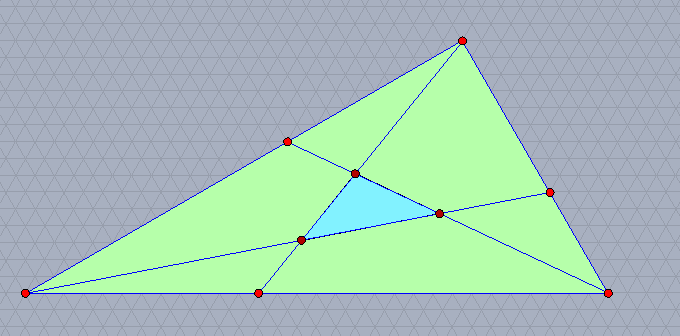
向きを揃えなければ，また面積が変わってくる。
三角形の各辺の三等分点と，それぞれに向かい合う頂点を，向きを揃えずに結ぶと，もとの三角形の1/70の面積の三角形ができる。向きを揃えたときの1/10の面積に。

五等分点になると，だいぶ数字が汚くなってくる。
三角形の各辺の五等分点（頂点に近いもの）と，それぞれに向かい合う頂点を，向きを揃えずに結ぶと，もとの三角形の2/63の面積の三角形ができる。向きを揃えたときの2/27の面積。

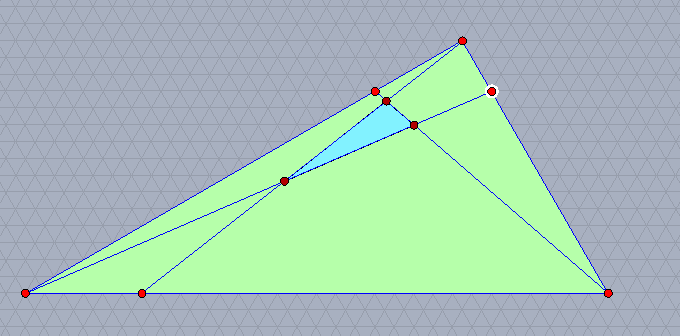
とりあえず最後。
三角形の各辺の五等分点（頂点から遠いもの）と，それぞれに向かい合う頂点を，向きを揃えずに結ぶと，もとの三角形の3/532の面積の三角形ができる。向きを揃えたときの3/28の面積。