焼きなまし法の適用メモ
はじめに
焼きなまし法について、問題へ適用する際のメモ。
焼きなまし法とは
- Simulated Annealing, SA
- 物理現象の焼きなましのコンセプトを組み合わせ最適化問題の探索過程に導入した、確率的近似解法の一つ
- 現在の解の近傍から良い解に移動することを繰り返す「局所探索」に対して、悪くなる解への移動を繰り返し回数や悪化の度合いに依存する確率で許すことで、局所最適解から脱出することがポイント
- 以前のメモ
疑似コード
x:=初期解, T:=初期温度, R:=初期イテレーション回数
while 終了条件 do begin
for i:=1 to R do begin
y:=近傍解の一つ(y∈N(x))
Δ:=score(y) - score(x)
if Δ >= 0 then x:=y; else
if exp(-Δ/T) >= frand() then x:=y
end
T:=CalcTemp(T)
R:=CalcIter(R)
end
return 解;c++でのコーディング例: 診断人さん, 焼きなまし法のコツ, http://shindannin.hatenadiary.com/entry/20121224/1356364040
重要なパラメータ
近傍定義
- 解xの近傍集合N(x)をどのように定義するか?で解空間も変化しうる
- 時間制約などがある場合は特に効率的な探索ができるよう解空間の構造、近傍サイズなども考慮
- すべての実行解は、任意の実行解から到達可能、など
- 効率的な探索を行えるようにするためには以下のような構造の近傍を避けたり、別な探索手法など検討
- とげとげ、ぎざぎざ
- 深いくぼみ
- 平坦
- chokudai先生の焼きなまし講座, https://togetter.com/li/607979
- tsukammoさん, 競技プログラミングにおいて焼きなまし法に堕ちずに落とすコツ, https://qiita.com/tsukammo/items/b410f3202372fe87c919
冷却スケジュール
- 初期温度T
- 十分高い温度から始めるべき
- ただし、場合によっては良い初期解&低い温度にしてもよい可能性もある?
- 温度の減少関数CalcTemp
- 十分ゆっくり冷却させる
- 冷却速度が時間に依る/依らない関数、複雑な速度変化の関数など様々考えられる
- 例:T_k = r^k * 初期温度(ただし、r=0.8〜0.99程度)、T_k = 初期温度 / log_2(k+2)、など
- 各温度での反復回数R
- 近傍をまんべんなく探索できることが求められるが、近傍定義に依るのでそっちのほうが重要
- 終了条件
- 制限時間、解のスコアの変動がなくなる(小さくなる)、など
細かいチューニング
- 高速化
- 探索回数が稼げた方がよいので、スコア計算を差分でできるようにする、無駄な計算を省略するなどは重要
- スコア関数の見直し
- 解xでのスコアは直接的な評価値でなくても、状態の良い悪いの加点減点、整数ではなく小数、など工夫が可能
- 遷移確率の見直し
- 温度と悪化具合を考慮した確率であればよさそう
- 焼きなまし処理終了後の探索
- 最後に近傍付近で部分的に探索したり、など
- 時間を延ばしてスコアが伸びるか?の確認
- tomerunさん, 北大日立新概念マラソンでやった高速化色々, http://topcoder.g.hatena.ne.jp/tomerun/20171216/1513436397
- 診断人さん, 焼きなまし法のコツ, http://shindannin.hatenadiary.com/entry/20121224/1356364040
- tsukammoさん, 競技プログラミングにおいて焼きなまし法に堕ちずに落とすコツ, https://qiita.com/tsukammo/items/b410f3202372fe87c919
考え方、考えるべき点など
焼きなまし法を適用するべきかどうか
問題ごとの考察が重要だが、以下の概念や知見が役に立つ。
「文脈」
- colunさん, https://twitter.com/colun/status/645318121713078272
- colunさんのマラソンマッチ関連の話, https://togetter.com/li/876191
- hoshi524さん, 北大日立マラソン1stで考えるマラソン入門, http://hoshi524.hatenablog.com/entry/2017/12/01/043534
- TCO16 MM R3, https://togetter.com/li/990736?page=50
- colunさん, 焼きなまし法の真実, http://www.colun.net/archives/774
問題のタイプ
- マラソンマッチ談義, https://togetter.com/li/516809
- tsukammoさん, 競技プログラミングにおいて焼きなまし法に堕ちずに落とすコツ, https://qiita.com/tsukammo/items/b410f3202372fe87c919
有名アルゴリズムの適用に囚われない
- takapt0226さん, Topcoderマラソンマッチの探索問題で重要なこと, https://qiita.com/takapt0226/items/b2f6d1d77a034b529e21
- not522さん, ナップサック問題でマラソンマッチ入門, http://not522.hatenablog.com/entry/2016/03/20/005946
- greedyでもよい解を生成する
その他、概念とか用語とか
疑似平衡
- 理論的な解析として、解の移動系列を確率過程としてのマルコフ連鎖と捉えて収束性が議論されるらしい
- 反復は定常状態になるまで行える場合、かつ、温度をT→0にしていく場合、確率的に最適解に収束することが示される
- 反復回数の限度を与える場合、温度パラメータの系列が十分ゆっくり冷却されるならば、収束が保証される
- しかし、理論的に必要となる計算時間は膨大になりすぎてしまうので、実用的には(理論的枠組みからは外れるが)「各温度で、できるかぎり平衡に近い状態(疑似平衡)」を得られるようにチューニングすることが重要なポイントになるよう
受理率
- ある温度Tでの全反復数に対して、実際に受理され移動が発生した回数の比率
- η(T) = (温度Tでの移動回数) / (温度Tでの反復回数)
- 受理率が低い場合、山登りと同様に局所最適解からの脱出が困難になってしまう
- 場合によると思われるが、0.3〜0.5ぐらいだと効率の良い探索が行われるとのこと
近接最適性原理
- 「良い解同士は何らかの類似構造を持っている」という経験的な原理
- ある良い解と別の良い解の共通要素が多い、みたいな場合もこの原理が成り立つ
- この原理が成り立つような解の偏りがあるならば、この類似構造を活用して効率的に最適解を探索できる可能性がある
集中化と多様化
- 集中化
- 「良い解の近傍により良い解が存在する」をもとに、良い解の近くを重点的に探索する戦略
- 多様化
- より遠くにある良い解を見つける戦略
- 焼きなましの場合、温度や近傍構造などでこの集中化・多様化のチューニングや工夫をすることができる
RangeCoderを試す
はじめに
RangeCoderのメモ。
中途半端な理解で適当に書き写そうとしたらひどいことになったので、まとめておく。。。
RangeCoderとは
- エントロピー符号の一種
- シンボル列をある数値で表現する
以下、桁上りありの場合について下記サイトを参考に作成してみた。
http://www.geocities.jp/m_hiroi/light/pyalgo36.html
他にも「桁上りなし」や「適応型」などがあるよう。
http://www.geocities.jp/m_hiroi/light/pyalgo37.html
アルゴリズム
範囲の拡大
- かなり大きい範囲を用意しておかないとすぐに範囲が狭まってしまってシンボルの出現確率で区分けするに十分な整数がなくなってしまう
- そこで、ある程度の大きさの範囲からスタートし、ある程度の大きさ以下になったら全体をx倍するような処理を繰り返すことで、これに対処する
実装方法
- 上記は多倍長などを用いなくても、普通の整数型を使って、都度、上位byteを出力してしまって、範囲を表す変数を常にある程度の大きさに収まるようにすることで実装できる
- 範囲の最大値max_range、拡大する範囲の閾値min_range、範囲の左端をlow、範囲の幅をrangeとすると、上記で言っているのは「lowをmax_range以下に保つように実装する」ということ
- ここでは、以下のように定める
- max_rangeのバイト数をrange_byteとする
- min_rangeのバイト数はrange_byte-1
- 拡大率は0x100(256)倍
拡大処理に伴う問題
- 拡大処理を行うときに上位byteの出力に伴う問題がいくつかある
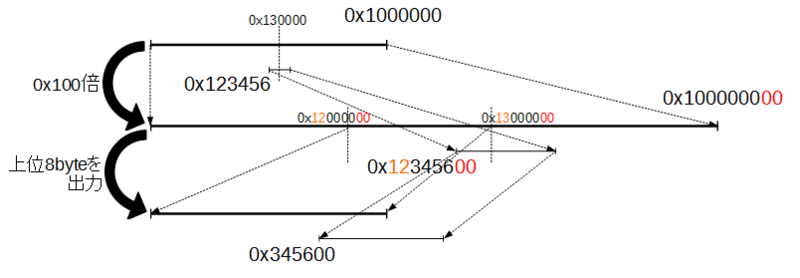
- 図で、low=0x123456のときrangeが小さくなりすぎて拡大したとする(lowとrangeをそれぞれ0x100倍)
- lowは0x12345600となるが、max_range以下に収まるようにしたいので、上位byteの0x12を出力してしまって、下位の0x345600を次のlowとする
- 問題は「出力済みの桁の繰り上げ(桁上り)が発生しうる」こと
桁上り
- 図で、単純に上位byteの0x12を出力してしまうと、次の範囲処理でmax_range=0x1000000を超えた場合、実は出力すべきは0x13だった、、、ということが起きうる
- また、拡大処理した際に出力byteが0xffだとさらに出力をさかのぼって桁上りを処理しなければならない
- 出力済みが「0x12, 0xff, 0xff, 0xff」で桁上りが発生したら「0x13,0x00,0x00,0x00」にしなければならない
- これの解決方法の一つとして、実際に出力はせずに「バッファにためる」ことで確定するまで出力を保留する方法がある
- 出力候補の先頭byteをbuff、後続の0xffの個数をcntとする
- 一つ目の「次の範囲処理max_rangeを超える場合」は、超えた場合にはrangeがmax_range以下であるため、桁上り分は+1しかならないので、buff++をして、lowはmax_range以下の部分だけにマスクすればよい
- このとき、cntが1個以上の場合は「0x12, 0xff, ..., 0xff」を+1すると「0x13, 0x00, ..., 0x00」のような状態に変化するので、最後の「0x00」以外は出力してしまって問題ない
- 二つ目の「拡大処理した際」は、出力候補のlowの上位bit部分が0xffなら桁上りがまだあり得るので出力はせずにcnt+1だけ、0xff未満ならbuffとcnt個分の0xffを出力してbuffにその値をいれてあげればよい
終了処理
- 残っているbuff,cnt,lowをすべて出力して終了
シンボルの出現頻度テーブル
- デコード処理ではシンボルの出現確率で区分けするために出現頻度テーブルも保存しておく
- 注意として、出現頻度の合計値はmin_range以下である必要がある
- そうでないとrangeを区分に分割するときに整数に割り当てられない場合ができてしまう
- 実装上は、頻度値をshort型などで持たせることで、頻度合計値をmin_range以下にしたり、テーブル保存時の容量削減をすると良いよう
デコード処理
- 出現頻度テーブルと出力した数値を頭から読み込んでいけばよい
- エンコード処理と同様に、rangeが小さくなりすぎたら拡大しながら読み込んでいく
コード
いくつかのデータで復元できているので、おそらく大丈夫。
#include <iostream> #include <vector> class RangeCoder { const int64_t range_byte = 6; //max_rangeのバイト数 const int size = 0x10000; //出現するデータの種類数の最大値(入力シンボルをuint16_tにしているため) const int64_t max_range = 0x1LL << (8 * range_byte); //rangeの最大幅 const int64_t min_range = 0x1LL << (8 * (range_byte-1)); //rangeを拡大する幅の閾値 const int64_t mask = max_range - 1; //max_range分のマスク(0xfff...fff) const int64_t shift = 8 * (range_byte-1); //出力分計算用(バッファ処理用「0xff00...00」生成と1byteずつの出力するため用) std::vector<int32_t> count, count_sum; //頻度分布、頻度累積分布 int32_t sum; //頻度合計値 int32_t orig_size; //入力シンボル数保存用 int pos; // 出力位置保存用 void init(){ for(int i=0; i<size; i++){ count[i] = 0; count_sum[i] = 0; } pos = 0; } //頻度分布、頻度累積分布の作成 void make_count(const std::vector<uint16_t>& in){ init(); for(uint16_t ch : in){ int chi = ch & 0xffff; count[chi]++; } //頻度値を16bitに抑えるため、頻度値全体を1/2^n倍する int32_t max_count = 0; for(int i=0; i<size; i++){ max_count = std::max(max_count, count[i]); } if(max_count > 0xffff){ int n = 0; while(max_count > 0xffff){ max_count >>= 1; n++; } for(int i=0; i<size; i++){ if(count[i] > 0){ count[i] >>= n; count[i] |= 1; } } } //頻度合計値はmin_range以下にしなければいけないので、 //抑えるための処理(1/2を繰り返す) //注意: 無限ループに入りうる while(true){ int32_t c_sum = 0; for(int i=0; i<size; i++){ c_sum += count[i]; } if(c_sum < min_range) break; for(int i=0; i<size; i++){ if(count[i] > 0){ count[i] >>= 1; if(count[i] == 0) count[i] = 1; } } } //頻度累積分布の作成 sum = 0; for(int i=0; i<size; i++){ count_sum[i+1] = sum + count[i]; sum += count[i]; } } //1byte分出力 void putc(std::vector<uint8_t>& ret, uint8_t c){ ret.push_back(c); } //1byte分読込 int getc(const std::vector<uint8_t>& in){ if(pos >= in.size()) return 0; return in[pos++] & 0xff; } //ヘッダ情報の出力 void save_header(std::vector<uint8_t>& ret, int32_t orig_size){ //シンボル数 putc(ret, (orig_size>>24) & 0xff); putc(ret, (orig_size>>16) & 0xff); putc(ret, (orig_size>>8) & 0xff); putc(ret, orig_size & 0xff); //頻度分布 int32_t num = 0; //シンボルのユニーク数 for(int i=0; i<size; i++) if(count[i] > 0) num++; putc(ret, (num>>24) & 0xff); putc(ret, (num>>16) & 0xff); putc(ret, (num>>8) & 0xff); putc(ret, num & 0xff); for(int i=0; i<size; i++){ if(count[i] > 0){ //シンボル番号 putc(ret, (i>>8) & 0xff); putc(ret, i & 0xff); //シンボルの出現頻度 putc(ret, (count[i]>>8) & 0xff); putc(ret, count[i] & 0xff); } } } //ヘッダ情報の読込 void load_header(const std::vector<uint8_t>& in){ init(); //シンボル数 orig_size = getc(in); orig_size <<= 8; orig_size |= getc(in); orig_size <<= 8; orig_size |= getc(in); orig_size <<= 8; orig_size |= getc(in); //頻度分布 int32_t num = getc(in); num <<= 8; num |= getc(in); num <<= 8; num |= getc(in); num <<= 8; num |= getc(in); for(int i=0; i<num; i++){ //シンボル番号 int32_t id = getc(in); id <<= 8; id |= getc(in); //シンボルの出現頻度 int32_t cnt = getc(in); cnt <<= 8; cnt |= getc(in); count[id] = cnt; } //頻度累積分布の作成 sum = 0; for(int i=0; i<size; i++){ count_sum[i+1] = sum + count[i]; sum += count[i]; } } //デコード用範囲から該当するシンボルの探索 int32_t search_code(int32_t val){ int32_t i = 0; int32_t j = size-1; while(i < j){ int32_t k = (i + j) / 2; if(count_sum[k+1] <= val){ i = k + 1; }else{ j = k; } } return i; } public: RangeCoder():count(size+1, 0), count_sum(size+1, 0){} std::vector<uint8_t> encode(const std::vector<uint16_t>& in){ std::vector<uint8_t> ret; make_count(in); save_header(ret, in.size()); //桁上りバッファ用 // buff: 出力候補 // cnt: buff以降に続く出力候補0xffの数 // => [0x12, 0xff, 0xff, ..., 0xff]のような情報 int64_t buff = 0, cnt = 0; //範囲計算用 int64_t low = 0, range = max_range; //下限と範囲 for(int i=0; i<in.size(); i++){ //入力シンボル int32_t ch = in[i] & 0xffff; //該当範囲の計算 int64_t temp = range / sum; low += count_sum[ch] * temp; range = count[ch] * temp; //桁上りの処理 //該当範囲がmax_rangeを超えてしまった場合 if(low >= max_range){ buff++; low &= mask; //もしcntが0より大きければ、[0x12,0xff,0xff...,0xff]のような状態なので、 //buffが+1されたことで[0x13,0x00,0x00...,0x00]のようになり、最後の0x00以外は出力してよい if(cnt > 0){ putc(ret, buff & 0xff); //buffの出力 for(int j=0; j<cnt-1; j++) putc(ret, 0x00); //0x00をcnt-1個分出力、最後の0x00はbuffとする buff = 0x00; cnt = 0x00; } } //範囲が小さくなったら全体をを拡大(256倍) while(range < min_range){ //拡大することでmax_rangeを超える上位1バイト分が、 // - 0xffより小さければ上位8bitは0xffではないので、 // バッファを出力して、その上位8bit分をbuffにいれる(rangeは範囲内なので0xfe以下なら絶対に0xffまでしかいかない) // - 0xffの場合は、まだ桁上りがあるかもしれないので、0xffを増やす意味でcntを+1する if(low < (0xffLL << shift)){ //low < 0xff000...000 putc(ret, buff & 0xff); for(int j=0; j<cnt; j++) putc(ret, 0xff); buff = (low >> shift) & 0xff; cnt = 0; }else{ cnt++; } //全体を256倍に拡大する low = (low << 8) & mask; range <<= 8; } } //最後に残っている情報(buff, cnt, low)をすべて出力 int32_t ch = 0xff; if(low >= max_range){ buff++; ch = 0; } putc(ret, buff & 0xff); for(int j=0; j<cnt; j++) putc(ret, ch & 0xff); for(int j=shift; j>=0; j-=8){ putc(ret, (low >> j) & 0xff); } return ret; } std::vector<uint16_t> decode(const std::vector<uint8_t>& in){ std::vector<uint16_t> ret; load_header(in); getc(in); int64_t range = max_range; int64_t low = 0; for(int i=shift; i>=0; i-=8){ low |= getc(in); if(i>0) low <<= 8; } while(ret.size() < orig_size){ int64_t temp = range / sum; int32_t ch = search_code(low / temp); low -= temp * count_sum[ch]; range = temp * count[ch]; while(range < min_range){ range <<= 8; low = ((low << 8) + getc(in)) & mask; } ret.push_back( ch & 0xffff ); } return ret; } }; int main(){ RangeCoder encoder, decoder; //入力シンボル列 std::vector<uint16_t> v; for(int i=0; i<10; i++){ v.push_back(4); v.push_back(3); v.push_back(2); v.push_back(2); v.push_back(1); v.push_back(1); v.push_back(1); v.push_back(1); } //エンコード std::cout << "encoding" << std::endl; std::vector<uint8_t> encode_code = encoder.encode(v); std::cout << v.size() * 16 << " => " << encode_code.size() * 8 << std::endl; //デコード std::cout << "decoding" << std::endl; std::vector<uint16_t> decode_code = decoder.decode(encode_code); //結果の確認 for(int i=0; i<decode_code.size(); i++){ std::cout << i << "\t" << v[i] << "\t" << decode_code[i] << std::endl; } return 0; }
結果
encoding 1280 => 384 decoding 0 4 4 1 3 3 2 2 2 3 2 2 4 1 1 5 1 1 6 1 1 7 1 1 8 4 4 ...
1280bitのシンボル列を384bitに圧縮できているよう。
上記、書き換え不可能な出力ではなく、入れた後で書き換え可能な出力用vectorに入れているので、素直に桁上げしにいく処理にした方がコードは短くなりそう。
Elias-Fano Encodingで遊ぶ
はじめに
読んでる論文に出てきてたElias-Fano Encodingをちょっと書いて遊んでみた。
Elias-Fano Encodingとは
- 単調増加整数列の表現方法のひとつ
- 他の方法としては、ちょっと情報が古いけど http://d.hatena.ne.jp/jetbead/20110918/1316373030 など
- 厳密にはsuccinctではないが、succinctに近い表現
- quasi-succinct representationと言っている
- 整数列の各値を「上位bit列」と「下位bit列」に分割し、整数列全体では、上位bit列を「(negated) unary code表現」、下位bit列を「各下位bitを連結したbit列」で表現したもの
- 上位、下位のbit数は等分ではなく、上位bitがceil(lg(n))個
- 例: {3,4,5}という整数列の場合
- ceil(lg(3))=2として、上位2bitと下位1bitに分ける
- 3は011、4は100、5は101なので、上位bitは01と10と10、下位bitは1と0と1
- 上位bit列はnegated unary codeで表現するので、00が0回、01が1回、10が2回、11が0回なので、「0101100」と表現する
- 1^{00の個数}0 1^{01の個数}0 1^{10の個数}0 ...と表現
- 下位bit列は、連結するので「101」と表現
- 転置インデクスやグラフ、Trieなどの表現として利用する論文が発表されているよう
- 有用なコードもgithubで公開されているので実用する場合はそちらを参照
コード
http://pages.di.unipi.it/pibiri/slides/seminar_ef.pdf
を参考に「正の整数の単調増加列(1以上の整数、同じ整数はなし、ソート済み)」を想定した場合のElias-Fano Encodingするコードを書いてみた。
操作は「access: S[i]の値」と「successor(x): min{S[i] | S[i] >= x}」の2つ。
いくつかのランダムケースで試して問題なさそうなことまでしか確認していない。
#include <vector> #include <map> #include <cstdint> #include <algorithm> #include <iostream> #include <cmath> class FID { static const int BIT_SIZE = 64; using BLOCK_TYPE = uint64_t; int size; int block_size; std::vector<BLOCK_TYPE> blocks; std::vector<int> s_rank, s0_rank; public: BLOCK_TYPE popcount(BLOCK_TYPE x){ x = ((x & 0xaaaaaaaaaaaaaaaaULL) >> 1) + (x & 0x5555555555555555ULL); x = ((x & 0xccccccccccccccccULL) >> 2) + (x & 0x3333333333333333ULL); x = ((x & 0xf0f0f0f0f0f0f0f0ULL) >> 4) + (x & 0x0f0f0f0f0f0f0f0fULL); x = ((x & 0xff00ff00ff00ff00ULL) >> 8) + (x & 0x00ff00ff00ff00ffULL); x = ((x & 0xffff0000ffff0000ULL) >> 16) + (x & 0x0000ffff0000ffffULL); x = ((x & 0xffffffff00000000ULL) >> 32) + (x & 0x00000000ffffffffULL); return x; } public: FID(int size): size(size), block_size(((size + BIT_SIZE - 1) / BIT_SIZE) + 1), blocks(block_size, 0), s_rank(block_size, 0), s0_rank(block_size, 0) {} void init(int sz){ blocks.clear(); s_rank.clear(); size = sz; block_size = ((size + BIT_SIZE - 1) / BIT_SIZE) + 1; blocks.resize(block_size, 0); s_rank.resize(block_size, 0); s0_rank.resize(block_size, 0); } void set(int i){ blocks[i/BIT_SIZE] |= 1ULL << (i%BIT_SIZE); } void finalize(){ s_rank[0] = 0; for(int i=1; i<block_size; i++){ s_rank[i] = s_rank[i-1] + popcount(blocks[i-1]); } s0_rank[0] = 0; for(int i=1; i<block_size; i++){ s0_rank[i] = s0_rank[i-1] + (BIT_SIZE - popcount(blocks[i-1])); } } bool access(int i){ return (blocks[i/BIT_SIZE] >> (i%BIT_SIZE)) & 1ULL; } int rank(int i){ BLOCK_TYPE mask = (1ULL << (i%BIT_SIZE)) - 1; return s_rank[i/BIT_SIZE] + popcount(mask & blocks[i/BIT_SIZE]); } int select(int x){ if(rank((block_size-1) * BIT_SIZE) <= x) return -1; int lb = 0, ub = block_size-1; while(ub-lb>1){ int m = (lb+ub)/2; if(s_rank[m]<=x) lb = m; else ub = m; } int lbb = lb*BIT_SIZE, ubb = (lb+1)*BIT_SIZE; while(ubb-lbb>1){ int m = (lbb+ubb)/2; if(rank(m)<=x) lbb = m; else ubb = m; } return lbb; } int select0(int x){ if((block_size-1) * BIT_SIZE - rank((block_size-1) * BIT_SIZE) <= x) return -1; int lb = 0, ub = block_size-1; while(ub-lb>1){ int m = (lb+ub)/2; if(s0_rank[m]<=x) lb = m; else ub = m; } int lbb = lb*BIT_SIZE, ubb = (lb+1)*BIT_SIZE; while(ubb-lbb>1){ int m = (lbb+ubb)/2; if(m-rank(m)<=x) lbb = m; else ubb = m; } return lbb; } }; class EliasFano { uint32_t n, u, lgn, lgun; FID low, high; //ceil(lg(x)) uint32_t ceillg(double x){ return ceil(log(x)/log(2)); } uint32_t low_get(size_t i){ uint32_t ret = 0; for(uint32_t p=0; p<lgun; p++){ ret |= (low.access(lgun*i+p)) << (lgun-1-p); } return ret; } public: EliasFano():low(0),high(0){} size_t size(){ return n; } void build(const std::vector<uint32_t>& v){ if(v.size() == 0) return; n = v.size(); u = v.back(); lgun = ceillg(u/(double)n); lgn = ceillg(u+1) - lgun; {//low bits low.init(lgun * n); int pos = lgun * n - 1; for(auto it=v.rbegin(); it!=v.rend(); ++it){ for(uint32_t b=0; b<lgun; b++){ if(((*it)>>b)&1){ low.set(pos); } pos--; } } low.finalize(); } {//high bits high.init((1<<lgn) + n); std::vector<uint32_t> cnt(1<<lgn, 0); for(uint32_t x : v){ cnt[(x>>lgun)]++; } int pos = 0; for(uint32_t x : cnt){ for(uint32_t i=0; i<x; i++){ high.set(pos); pos++; } pos++; } high.finalize(); } } uint32_t access(int i){ if(n == 0) return 0; uint32_t ret = 0; ret |= (high.select(i) - i) << lgun; ret |= low_get(i); return ret; } uint32_t successor(uint32_t x){ if(n == 0) return 0; if(u < x) return 0; uint32_t h = (x>>lgun); uint32_t l = x&((1<<lgun)-1); uint32_t p1 = (h==0)?0:(high.select0(h-1)-h+1); uint32_t p2 = high.select0(h)-h; if(x <= access(p1)) return access(p1); while(p2-p1>1){ uint32_t m = (p2+p1)/2; if(low_get(m) < l) p1 = m; else p2 = m; } return access(p2); } void dump(){ std::cout << "n = " << n << ", "; std::cout << "u = " << u << ", "; std::cout << "ceil(lg(n)) = " << lgn << ", "; std::cout << "ceil(lg(u/n)) = " << lgun << std::endl; std::cout << "L = "; for(uint32_t i=0; i<lgun*n; i++){ if(low.access(i)) std::cout << 1; else std::cout << 0; } std::cout << std::endl; std::cout << "H = "; for(uint32_t i=0; i<(1<<lgn)+n; i++){ if(high.access(i)) std::cout << 1; else std::cout << 0; } std::cout << std::endl; } }; int main(){ //正の整数の単調増加列(1以上の整数, 同じ整数はなし, ソート済み) std::vector<uint32_t> v{3,4,7,13,14,15,21,43}; EliasFano ef; ef.build(v); ef.dump(); std::cout << "[access()]" << std::endl; for(size_t i=0; i<ef.size(); i++){ std::cout << i << "\t" << v[i] << "\t" << ef.access(i) << std::endl; } std::cout << "[successor()]" << std::endl; for(uint32_t x=0; x<50; x++){ std::cout << x << "\t" << ef.successor(x) << std::endl; } return 0; }
結果
プレゼンの例と同じになっていることを確認。
n = 8, u = 43, ceil(lg(n)) = 3, ceil(lg(u/n)) = 3 L = 011100111101110111101011 H = 1110111010001000 [access()] 0 3 3 1 4 4 2 7 7 3 13 13 4 14 14 5 15 15 6 21 21 7 43 43 [successor()] 0 3 1 3 2 3 3 3 4 4 5 7 6 7 7 7 8 13 9 13 10 13 11 13 12 13 13 13 14 14 15 15 16 21 17 21 18 21 19 21 20 21 21 21 22 43 23 43 24 43 25 43 26 43 27 43 28 43 29 43 30 43 31 43 32 43 33 43 34 43 35 43 36 43 37 43 38 43 39 43 40 43 41 43 42 43 43 43 44 0 45 0 46 0 47 0 48 0 49 0
XBWを試す
はじめに
XBWをWaveletMatrixを使って、試しに実装してみた。
XBWとは
- 効率よくTrie木を表現する方法
- Burrows-Wheeler Transform(BWT)の(木への)拡張
- 詳しい解説や作り方は以下のページや「高速文字列解析の世界」などを参照
コード
XBWでの表のソートはそのまま文字列同士のソートをしている。
チェックは、コード中にあるように、適当にkey文字列とkey文字列じゃないのを生成してtrieと結果が一緒になるかだけ。
WaveletMatrixの方で理解のためにいくつか関数を書いているけど、rank()ぐらいしか使っていないので、それ以外はあまりVerifyできていない。
(g++はバージョン「5.4.0」、オプション「-std=gnu++1y -O2」で実行してる)
#include <vector> #include <map> #include <cstdint> #include <algorithm> #include <iostream> #include <queue> #include <random> //完備辞書(Fully Indexable Dictionary) // 【使いまわすときの注意】 // - 全部set()したら、最後にfinalize()を呼ぶこと // - select(x)の実装で、xが要素数よりも多い場合-1を返す実装にしている // - 32bit/64bit書き換えは、BIT_SIZE,BLOCK_TYPE,popcount,整数リテラルのサフィックスなどを書き換えること class FID { static const int BIT_SIZE = 64; using BLOCK_TYPE = uint64_t; int size; int block_size; std::vector<BLOCK_TYPE> blocks; std::vector<int> s_rank; public: //for BIT_SIZE == 32 /* BLOCK_TYPE popcount(BLOCK_TYPE x){ x = ((x & 0xaaaaaaaa) >> 1) + (x & 0x55555555); x = ((x & 0xcccccccc) >> 2) + (x & 0x33333333); x = ((x & 0xf0f0f0f0) >> 4) + (x & 0x0f0f0f0f); x = ((x & 0xff00ff00) >> 8) + (x & 0x00ff00ff); x = ((x & 0xffff0000) >> 16) + (x & 0x0000ffff); return x; } */ //__builtin_popcount() //for BIT_SIZE == 64 BLOCK_TYPE popcount(BLOCK_TYPE x){ x = ((x & 0xaaaaaaaaaaaaaaaaULL) >> 1) + (x & 0x5555555555555555ULL); x = ((x & 0xccccccccccccccccULL) >> 2) + (x & 0x3333333333333333ULL); x = ((x & 0xf0f0f0f0f0f0f0f0ULL) >> 4) + (x & 0x0f0f0f0f0f0f0f0fULL); x = ((x & 0xff00ff00ff00ff00ULL) >> 8) + (x & 0x00ff00ff00ff00ffULL); x = ((x & 0xffff0000ffff0000ULL) >> 16) + (x & 0x0000ffff0000ffffULL); x = ((x & 0xffffffff00000000ULL) >> 32) + (x & 0x00000000ffffffffULL); return x; } //__builtin_popcountll() public: FID(int size): size(size), block_size(((size + BIT_SIZE - 1) / BIT_SIZE) + 1), blocks(block_size, 0), s_rank(block_size, 0){} void set(int i){ blocks[i/BIT_SIZE] |= 1ULL << (i%BIT_SIZE); } void finalize(){ s_rank[0] = 0; for(int i=1; i<block_size; i++){ s_rank[i] = s_rank[i-1] + popcount(blocks[i-1]); } } bool access(int i){ return (blocks[i/BIT_SIZE] >> (i%BIT_SIZE)) & 1ULL; } //iより前のビットが立っている個数 int rank(int i){ BLOCK_TYPE mask = (1ULL << (i%BIT_SIZE)) - 1; return s_rank[i/BIT_SIZE] + popcount(mask & blocks[i/BIT_SIZE]); } //x番目にビットが立っている位置 int select(int x){ if(rank((block_size-1) * BIT_SIZE) <= x) return -1; //注意 int lb = 0, ub = block_size-1; while(ub-lb>1){ int m = (lb+ub)/2; if(s_rank[m]<=x) lb = m; else ub = m; } int lbb = lb*BIT_SIZE, ubb = (lb+1)*BIT_SIZE; while(ubb-lbb>1){ int m = (lbb+ubb)/2; if(rank(m)<=x) lbb = m; else ubb = m; } return lbb; } }; //ウェーブレット行列(Wavelet Matrix) // 【使いまわすときの注意】 // - 全部set()したら、最後にfinalize()を呼ぶこと // - 32bit/64bit書き換えは、BIT_SIZE,VAL_TYPEなどを書き換えること class WaveletMatrix { static const int BIT_SIZE = 8; using VAL_TYPE = uint8_t; int size; std::vector<VAL_TYPE> v; std::vector<FID> matrix; std::vector<int> sep; struct mytuple { int b, s, e; mytuple(int b, int s, int e):b(b),s(s),e(e){} bool operator<(const mytuple& x) const { return e-s < x.e-x.s; } }; public: WaveletMatrix(int size): size(size), v(size, 0), matrix(BIT_SIZE, FID(size)), sep(BIT_SIZE, 0){} void set(int i, VAL_TYPE val){ v[i] = val; } void finalize(){ std::vector<VAL_TYPE> w(v.size(), 0); for(int b=BIT_SIZE-1; b>=0; b--){ for(int i=0; i<size; i++){ if((v[i] >> b) & 1ULL) matrix[b].set(i); else sep[b]++; } int b1=0, b2=sep[b]; for(int i=0; i<size; i++){ if((v[i] >> b) & 1ULL) w[b2++] = v[i]; else w[b1++] = v[i]; } for(int i=0; i<size; i++){ v[i] = w[i]; } matrix[b].finalize(); } } //元の配列のi番目の要素 VAL_TYPE access(int i){ VAL_TYPE ret = 0; for(int b=BIT_SIZE-1; b>=0; b--){ if(matrix[b].access(i)){ i = sep[b] + matrix[b].rank(i); ret = (ret << 1) + 1ULL; }else{ i = i - matrix[b].rank(i); ret = (ret << 1); } } return ret; } //[0,i)の範囲にxが何個存在するか int rank(int i, VAL_TYPE x){ int lb = 0, ub = i; for(int b=BIT_SIZE-1; b>=0; b--){ if((x >> b) & 1ULL){ lb = matrix[b].rank(lb); ub = matrix[b].rank(ub); lb += sep[b]; ub += sep[b]; }else{ lb = lb - matrix[b].rank(lb); ub = ub - matrix[b].rank(ub); } } return ub - lb; } //i番目(0-index)のxが出現する位置 int select(int i, VAL_TYPE x){ int lb = 0, ub = size; while(ub-lb>1){ int m = (lb+ub)/2; if(rank(m, x)<=i) lb = m; else ub = m; } return lb; } //[s,e)の範囲を切り出してソートしたときのn番目(0-index)の要素 VAL_TYPE quantile(int s, int e, int n){ for(int b=BIT_SIZE-1; b>=0; b--){ int zn = (e - s) - (matrix[b].rank(e) - matrix[b].rank(s)); if(zn <= n){ s = matrix[b].rank(s); e = matrix[b].rank(e); s += sep[b]; e += sep[b]; n = n - zn; }else{ s = s - matrix[b].rank(s); e = e - matrix[b].rank(e); } } return v[s]; } //[s,e)の範囲で出現回数が多い数値順に、その数値と出現回数のTop-K std::vector<std::pair<VAL_TYPE,int>> top_k(int s, int e, int k){ std::vector<std::pair<VAL_TYPE,int>> ret; std::priority_queue<mytuple> que; que.push(mytuple(BIT_SIZE-1,s,e)); while(!que.empty()){ mytuple q = que.top(); que.pop(); int b = q.b, st = q.s, en = q.e; if(b < 0){ ret.push_back(std::make_pair(v[st], en-st)); if((int)ret.size() >= k) break; }else{ int os = matrix[b].rank(st) + sep[b]; int oe = matrix[b].rank(en) + sep[b]; int zs = st - matrix[b].rank(st); int ze = en - matrix[b].rank(en); if(ze-zs > 0) que.push(mytuple(b-1,zs,ze)); if(oe-os > 0) que.push(mytuple(b-1,os,oe)); } } return ret; } //[s,e)の範囲でx<=c<yを満たすような数値cの合計出現数 int rangefreq(int s, int e, VAL_TYPE x, VAL_TYPE y){ int ret = 0; std::queue<std::pair<mytuple,VAL_TYPE>> que; que.push(std::make_pair(mytuple(BIT_SIZE-1,s,e),0)); while(!que.empty()){ std::pair<mytuple,VAL_TYPE> q = que.front(); que.pop(); int b = q.first.b, st = q.first.s, en = q.first.e; VAL_TYPE mn = q.second; VAL_TYPE mx = q.second | ((b>=0)?0:((-1ULL) >> (BIT_SIZE - 1 - b))); if(x <= mn && mx < y){ ret += en-st; } else if(mx < x || y <= mn){ continue; } else { if(b < 0) continue; int os = matrix[b].rank(st) + sep[b]; int oe = matrix[b].rank(en) + sep[b]; int zs = st - matrix[b].rank(st); int ze = en - matrix[b].rank(en); if(ze-zs > 0) que.push(std::make_pair(mytuple(b-1,zs,ze), q.second)); if(oe-os > 0) que.push(std::make_pair(mytuple(b-1,os,oe), q.second | (1ULL << b))); } } return ret; } }; //XBW class XBW { using VAL_TYPE = uint8_t; const char LAST_CHAR = (char)(0xff); struct Trie { bool flg; std::string rpp; std::map<char,Trie> next; Trie(){ flg = false; } void insert(const std::string &str){ Trie *r = this; for(size_t i=0; i<str.length(); i++){ r = &(r->next[str[i]]); } r->flg = true; } bool find(const std::string &str){ Trie *r = this; for(size_t i=0; i<str.length(); i++){ if(r->next.count(str[i]) == 0) return false; r = &(r->next[str[i]]); } return r->flg; } }; struct ST { std::string children; std::string rpp; ST(std::string children, std::string rpp):children(children),rpp(rpp){} bool operator<(const ST& x) const { return rpp < x.rpp; } }; Trie root; int xbw_size; std::string xbw_str; WaveletMatrix wm; FID fid; std::map<char,int> C; void build(std::vector<ST>& v){ //XBWのサイズと文字の出現数のカウント std::map<char,int> cnt; xbw_size = 0; for(size_t i=0; i<v.size(); i++){ xbw_size += v[i].children.length(); for(size_t j=0; j<v[i].children.length(); j++){ cnt[v[i].children[j]]++; } } //構築 wm = WaveletMatrix(xbw_size); fid = FID(xbw_size); int idx = 0; for(size_t i=0; i<v.size(); i++){ fid.set(idx); for(size_t j=0; j<v[i].children.length(); j++){ wm.set(idx, (VAL_TYPE)(v[i].children[j])); idx++; } } wm.finalize(); fid.finalize(); C[(char)(0)] = 1; for(int i=1; i<256; i++){ C[(char)(i)] = C[(char)(i-1)] + cnt[(char)(i-1)]; } //trieの削除 //root.next.clear(); } int rank(int i, VAL_TYPE x){ int pos = fid.select(i); return wm.rank(((pos<0)?xbw_size:pos),x); } public: XBW():wm(1),fid(1){} void add(const std::string& key){ root.insert(key); } void finalize(){ //chilren, reverse prefix pathの表の作成 std::vector<ST> v; std::queue<Trie*> que; que.push(&root); while(!que.empty()){ Trie *r = que.front(); que.pop(); std::string children; std::string rpp = r->rpp; for(std::map<char,Trie>::iterator it=(r->next).begin(); it!=(r->next).end(); ++it){ children += it->first; (it->second).rpp = rpp + it->first; que.push(&(it->second)); } if(r->flg){ children += LAST_CHAR; } std::reverse(rpp.begin(), rpp.end()); v.push_back(ST(children, rpp)); } std::sort(v.begin(), v.end()); //XBW文字列の作成 for(size_t i=0; i<v.size(); i++){ if(i>0) xbw_str += "|"; for(size_t j=0; j<v[i].children.length(); j++){ if(v[i].children[j] == LAST_CHAR) xbw_str += "__LAST__"; //表示の都合上 else xbw_str += v[i].children[j]; } } build(v); } std::string get_xbw_string(){ return xbw_str; } bool trie_find(const std::string& key){ return root.find(key); } bool find(const std::string& key){ int r = 0; for(size_t i=0; i<key.length(); i++){ if(rank(r+1,(VAL_TYPE)(key[i])) - rank(r,(VAL_TYPE)(key[i])) == 0) return false; r = C[key[i]] + rank(r,(VAL_TYPE)(key[i])); } if(rank(r+1,(VAL_TYPE)(LAST_CHAR)) - rank(r,(VAL_TYPE)(LAST_CHAR)) == 0) return false; return true; } }; int main(){ std::mt19937 rnd{ std::random_device()() }; std::map<std::string,int> keys, no_keys; int max_size = 500000; //keyとno_keysの要素数 int max_len = 40; //文字列の長さの最大値 int turn = 0; while(keys.size() < max_size || no_keys.size() < max_size){ //generate key string int len = rnd() % max_len + 1; std::string key = ""; for(int j=0; j<len; j++){ key += (char)(' ' + rnd()%95); } if(keys.count(key) != 0 || no_keys.count(key) != 0) continue; if(turn == 0 && keys.size() < max_size){ keys[key] = 1; turn = 1 - turn; } else if(turn == 1 && no_keys.size() < max_size){ no_keys[key] = 1; turn = 1 - turn; } } std::cout << "key generated..." << std::endl; XBW xbw; for(const auto& x : keys){ xbw.add(x.first); } xbw.finalize(); std::cout << "XBW built..." << std::endl; //std::cout << "XBW = " << xbw.get_xbw_string() << std::endl; bool error = false; for(const auto& x : keys){ if(xbw.trie_find(x.first) != xbw.find(x.first)){ std::cout << "error : " << x.first << std::endl; error = true; } } for(const auto& x : no_keys){ if(xbw.trie_find(x.first) != xbw.find(x.first)){ std::cout << "error : " << x.first << std::endl; error = true; } } if(!error) std::cout << "no error" << std::endl; return 0; }
確認のために、解説ページのTrieからXBWを出力してみる。
main()の内容を以下のように変更すると確認できる。
int main(){ std::vector<std::string> v{"to","tea","ten","i","in","inn","we"}; XBW xbw; for(const auto& x : v){ xbw.add(x); } xbw.finalize(); std::cout << xbw.get_xbw_string() << std::endl; return 0; }
結果。
itw|__LAST__|an|__LAST__|n__LAST__|__LAST__|n__LAST__|__LAST__|__LAST__|eo|e
Kneser-Ney smoothingで遊ぶ
はじめに
100-nlp-papersで紹介されてた一番最初の論文に、クナイザーネイスムージングのスッキリな実装が載っていたので書いてみる。
Joshua Goodman: A bit of progress in language modeling, MSR Technical Report, 2001.
Kneser-Ney smoothingとは
- 言語モデルのスムージング(平滑化)手法の一種で、高い言語モデル性能を実現している
- ニューラル言語モデルでも比較によく使われる
- アイデアとしては「(n-1)-gramが出現した文脈での異なり数」を使うこと
- 頻度を使うと、高頻度なn-gramではその(n-1)-gramも多くなってしまうため、特定文脈でしかでないような(n-1)-gramに対しても高い確率値ことになっていて、歪んだ結果になってしまう
- 「San Francisco」の頻度が多いと「Francisco」の頻度も高くなるが、P(Francisco|on)とかはあまり出現しないので低くなってほしいところ、「Franciscoの頻度」を使って確率値を推定すると高くなってしまう
- 頻度ではなく、異なり数で(n-1)-gramの確率を推定することで、補正する
- 頻度を使うと、高頻度なn-gramではその(n-1)-gramも多くなってしまうため、特定文脈でしかでないような(n-1)-gramに対しても高い確率値ことになっていて、歪んだ結果になってしまう
- 上のレポートでは、Interpolatedな補間方法での実装例を紹介している
- back-offな方法も考えらえる
- discount(割引値)パラメータをn-gramごとに分けた方法は「modified Kneser-Ney smoothing」と呼ばれている
UNKの扱い
- レポートのAppendixのFigure17と18はそのままだと学習データに出現しない単語UNKが出てくると、unigramが0なので、確率も0になってしまう
- レポートの8ページ目では、一様分布1/|V|(Vは語彙集合)を使ってスムージングしてこれを避けると紹介されている
- λはどうするの?というのは、以下のページで議論されているように、λ(ε)と考えると、「λ==discountパラメータ」としてもよいかなと思うので、コードではそのようにした
コード
UNKのためにちょっと修正した。あんまりちゃんとチェックできていないけど、それっぽい数値を返しているのでおそらく大丈夫。
#include <iostream> #include <fstream> #include <vector> #include <string> #include <cmath> #include <unordered_map> class InterpolatedKneserNeyTrigram { const std::string delim = "\t"; double discount; //(0,1)の範囲で指定する std::unordered_map<std::string,int> TD, TN, TZ, BD, BN, BZ, UN; int UD; public: InterpolatedKneserNeyTrigram():discount(0.1),UD(0){} InterpolatedKneserNeyTrigram(double d):discount(d),UD(0){} //ファイルに書き出し void save(const std::string& filename){ std::ofstream fout(filename); if(!fout){ std::cerr << "cannot open file" << std::endl; return; } fout << discount << std::endl; fout << TD.size() << std::endl; std::unordered_map<std::string,int>::iterator it; for(it=TD.begin(); it!=TD.end(); ++it) fout << it->first << std::endl << it->second << std::endl; fout << TN.size() << std::endl; for(it=TN.begin(); it!=TN.end(); ++it) fout << it->first << std::endl << it->second << std::endl; fout << TZ.size() << std::endl; for(it=TZ.begin(); it!=TZ.end(); ++it) fout << it->first << std::endl << it->second << std::endl; fout << BD.size() << std::endl; for(it=BD.begin(); it!=BD.end(); ++it) fout << it->first << std::endl << it->second << std::endl; fout << BN.size() << std::endl; for(it=BN.begin(); it!=BN.end(); ++it) fout << it->first << std::endl << it->second << std::endl; fout << BZ.size() << std::endl; for(it=BZ.begin(); it!=BZ.end(); ++it) fout << it->first << std::endl << it->second << std::endl; fout << UN.size() << std::endl; for(it=UN.begin(); it!=UN.end(); ++it) fout << it->first << std::endl << it->second << std::endl; fout << UD << std::endl; fout.close(); } //ファイルから読み込み void load(const std::string& filename){ std::ifstream fin(filename); if(!fin){ std::cerr << "cannot open file" << std::endl; return; } fin >> discount; int td, tn, tz, bd, bn, bz, un; std::string s; int c; fin >> td; for(int i=0; i<td; i++){ getline(fin,s); getline(fin, s); fin >> c; TD[s] = c; } fin >> tn; for(int i=0; i<tn; i++){ getline(fin,s); getline(fin, s); fin >> c; TN[s] = c; } fin >> tz; for(int i=0; i<tz; i++){ getline(fin,s); getline(fin, s); fin >> c; TZ[s] = c; } fin >> bd; for(int i=0; i<bd; i++){ getline(fin,s); getline(fin, s); fin >> c; BD[s] = c; } fin >> bn; for(int i=0; i<bn; i++){ getline(fin,s); getline(fin, s); fin >> c; BN[s] = c; } fin >> bz; for(int i=0; i<bz; i++){ getline(fin,s); getline(fin, s); fin >> c; BZ[s] = c; } fin >> un; for(int i=0; i<un; i++){ getline(fin,s); getline(fin, s); fin >> c; UN[s] = c; } fin >> UD; fin.close(); } void set_discount(double d){ discount = d; } double get_discount() const { return discount; } void add_sentence(const std::vector<std::string>& sentence){ std::string w2 = "", w1 = ""; for(size_t i=0; i<sentence.size(); i++){ std::string w0 = sentence[i]; TD[ w2 + delim + w1 ]++; if(TN[ w2 + delim + w1 + delim + w0 ]++ == 0){ TZ[ w2 + delim + w1 ]++; BD[ w1 ]++; if(BN[ w1 + delim + w0 ]++ == 0){ BZ[ w1 ]++; UD++; UN[ w0 ]++; } } w2 = w1; w1 = w0; } } double prob(const std::vector<std::string>& sentence){ std::string w2 = "", w1 = ""; double ret = 0; for(size_t i=0; i<sentence.size(); i++){ std::string w0 = sentence[i]; double prob = 0; //そのままだとUN[w0]==0のときprob==0になるため、1/|V|を使うように変更 double uniform = 1.0 / UN.size(); double unigram = 0.0; if(UN.count( w0 ) > 0){ unigram = (UN[ w0 ] - discount) / (double)UD; } unigram += discount * uniform; if(BD.count( w1 ) > 0){ double bigram = 0; if(BN.count( w1 + delim + w0 ) > 0){ bigram = (BN[ w1 + delim + w0 ] - discount) / BD[ w1 ]; } bigram += BZ[ w1 ] * discount / BD[ w1 ] * unigram; if(TD.count( w2 + delim + w1 ) > 0){ double trigram = 0; if(TN.count( w2 + delim + w1 + delim + w0 ) > 0){ trigram = (TN[ w2 + delim + w1 + delim + w0 ] - discount) / TD[ w2 + delim + w1 ]; } trigram += TZ[ w2 + delim + w1 ] * discount / TD[ w2 + delim + w1 ] * bigram; prob = trigram; }else{ prob = bigram; } }else{ prob = unigram; } ret += log(prob); w2 = w1; w1 = w0; } return ret; } }; int main(){ InterpolatedKneserNeyTrigram lm; std::vector< std::vector<std::string> > train_v, valid_v; {//ファイルの読み込み std::ifstream trainfs("train.txt"); std::ifstream validfs("valid.txt"); std::string w; std::vector<std::string> tmp; while(trainfs >> w){ tmp.push_back(w); if(w == "EOS"){ train_v.push_back(tmp); tmp.clear(); } } tmp.clear(); while(validfs >> w){ tmp.push_back(w); if(w == "EOS"){ valid_v.push_back(tmp); tmp.clear(); } } } {//学習用の文を全部入れる for(size_t i=0; i<train_v.size(); i++){ lm.add_sentence(train_v[i]); } } {//よさそうなdを探す double best = log(0), best_d = 0; double prec = 0.001; for(double d=prec; d<1; d+=prec){ lm.set_discount(d); double logq = 0.0; for(size_t i=0; i<valid_v.size(); i++){ logq += lm.prob(valid_v[i]); } std::cerr << d << "\t" << logq << std::endl; if(best < logq){ best = logq; best_d = d; } } lm.set_discount(best_d); std::cerr << "best: " << best << " (d = " << best_d << ")" << std::endl; } lm.save("lm.data"); return 0; }
実験
データの準備
「坊ちゃん」の言語モデルを作ってみる。
青空文庫から「坊ちゃん」のテキストを取得し、「≪≫」などで囲まれた部分を削除したものを用意。
全部で470行で、10行ごとをdiscount係数確認用にする。
さらにそれを、mecab+ipadicで1行1単語にした以下のようなテキストを準備する。
(学習用train.txt 424行分、確認用valid.txt 46行分)
親譲り の 無鉄砲 で 小 供 の 時 から 損 ... と 答え た 。 EOS 親類 の もの ...
(1行分の終わりには「EOS」を含む)
事例
いくつかの例で確率を見てみる。
s=「親譲り の 無鉄砲 だ EOS」 → log(P(s)) = -23.7238
s=「親譲り の ブレイブハート だ EOS」 → log(P(s)) = -33.8758
s=「吾輩 は 猫 だ EOS」 → log(P(s)) = -36.8097
s=「無鉄砲 な フレンズ だ EOS」 → log(P(s)) = -38.3098
参考
- https://en.wikipedia.org/wiki/Kneser%E2%80%93Ney_smoothing
- 奥村, 自然言語処理シリーズ4 機械翻訳, コロナ社
- 徳永, 日本語入力を支える技術, 技術評論社
- https://www.youtube.com/watch?v=wtB00EczoCM
Inside-Outsideアルゴリズムを試す
はじめに
確率文脈自由文法での生成規則の適用確率の推定アルゴリズムで紹介されている「Inside-Outsideアルゴリズム」について、Webで検索してみても、最尤導出の構文木や内側確率の計算例などはあっても、外側確率や生成確率の推定などまで計算例を書いてくれているのはなさそうだったので、手計算確認用にプログラムを書いた。
Inside-Outsideアルゴリズムとは
コード
内側確率と外側確率、適用回数の推定が確認できればよいと思って書いたため、だいたい愚直。
最尤導出と内側確率が上の書籍と同じ値であるのと、繰り返し最適化で対数尤度が収束しているようなので、たぶん大丈夫。。。
(雑な確認しかしていないので、何かありましたら教えていただければと思います)
#include <iostream> #include <vector> #include <map> #include <string> #include <cmath> //乱数 // 注意: longではなくint(32bit)にすべき unsigned long xor128(){ static unsigned long x=123456789, y=362436069, z=521288629, w=88675123; unsigned long t; t=(x^(x<<11)); x=y; y=z; z=w; return w=(w^(w>>19))^(t^(t>>8)); } // 注意: int_maxぐらいで割るべき double frand(){ return xor128()%1000000/static_cast<double>(1000000); } double logsumexp(const std::vector<double>& lps){ if(lps.size() == 0) return -1e300; double mx = lps[0]; for(size_t i=0; i<lps.size(); i++){ if(lps[i] > mx) mx = lps[i]; } double sum = 0; for(size_t i=0; i<lps.size(); i++){ sum += exp(lps[i] - mx); } return mx + log(sum); } //計算用のdp[i][j][A]形式の3次元dpテーブル template<class T> class DPTable { int N; std::vector< std::vector< std::map<std::string,T> > > dp; public: DPTable(int N):dp(N, std::vector< std::map<std::string,T> >(N)){} bool exists(size_t i, size_t j, const std::string& S){ return dp[i][j].count(S) > 0; } T get(size_t i, size_t j, const std::string& S){ return dp[i][j][S]; } void set(size_t i, size_t j, const std::string& S, const T& val){ dp[i][j][S] = val; } std::vector<std::string> get_str_list(size_t i, size_t j){ std::vector<std::string> ret; for(typename std::map<std::string,T>::iterator itr = dp[i][j].begin(); itr != dp[i][j].end(); ++itr){ ret.push_back(itr->first); } return ret; } }; //文法< A -> B C, p > struct Grammar { std::string lhs; // A std::pair<std::string,std::string> rhs; // B C (lexicalならCは空) double lp; //確率値の対数 Grammar(const std::string lhs, const std::pair<std::string,std::string> rhs, double lp): lhs(lhs),rhs(rhs),lp(lp){} }; bool operator==(const Grammar& a, const Grammar& b){ return a.lhs == b.lhs && a.rhs == b.rhs; } bool operator<(const Grammar& a, const Grammar& b){ if(a.lhs == b.lhs) return a.rhs < b.rhs; return a.lhs < b.lhs; } //文法の管理 class Grammars { std::string start; std::map< std::pair<std::string,std::string>, std::vector<Grammar> > grammars; public: Grammars(std::string start = "S"):start(start){} void set_start(const std::string& st){ start = st; } std::string get_start(){ return start; } void add(const Grammar& grm){ grammars[grm.rhs].push_back(grm); } std::vector<Grammar> search(const std::pair<std::string,std::string>& rhs){ return grammars[rhs]; } //確率値を適当な値で埋める void fill_random(){ std::map< std::string,std::vector<double> > sum; for(std::map< std::pair<std::string,std::string>, std::vector<Grammar> >::iterator itr = grammars.begin(); itr != grammars.end(); ++itr){ for(size_t i=0; i<(itr->second).size(); i++){ (itr->second)[i].lp = log(frand() * 0.09 + 0.01);//0.01〜0.1で適当に与える(次の正規化でΣp(A->*)=1となるように調整する) sum[(itr->second)[i].lhs].push_back((itr->second)[i].lp); } } //正規化 std::map<std::string,double> norm; for(std::map< std::string,std::vector<double> >::iterator itr = sum.begin(); itr != sum.end(); ++itr){ norm[itr->first] = logsumexp(itr->second); } for(std::map< std::pair<std::string,std::string>, std::vector<Grammar> >::iterator itr = grammars.begin(); itr != grammars.end(); ++itr){ for(size_t i=0; i<(itr->second).size(); i++){ (itr->second)[i].lp -= norm[(itr->second)[i].lhs]; } } } std::vector<Grammar> get_all_grammar(){ std::vector<Grammar> ret; for(std::map< std::pair<std::string,std::string>, std::vector<Grammar> >::iterator itr = grammars.begin(); itr != grammars.end(); ++itr){ for(size_t i=0; i<(itr->second).size(); i++){ ret.push_back((itr->second)[i]); } } return ret; } void dump(){ for(std::map< std::pair<std::string,std::string>, std::vector<Grammar> >::iterator itr = grammars.begin(); itr != grammars.end(); ++itr){ for(size_t i=0; i<(itr->second).size(); i++){ Grammar grm = (itr->second)[i]; std::cout << grm.lhs << " -> " << grm.rhs.first << " " << grm.rhs.second << "\t" << exp(grm.lp) << std::endl; } } } }; class PCFG { public: //最尤導出計算用 struct Info { std::string lhs; std::pair<std::string,std::string> rhs; std::pair< std::pair<int,int>, std::pair<int,int> > idx; double delta; std::pair<int,int> ans; //結果パース用 Info():delta(-INF){} }; //Inside-Outside algorithm計算用 struct BetaAlpha { double beta; double alpha; BetaAlpha():beta(-INF),alpha(-INF){} BetaAlpha(double beta, double alpha):beta(beta),alpha(alpha){} }; private: static const double INF; //文法の管理 Grammars grammars; /* 最尤導出計算用 */ //dpテーブルから最尤な導出を配列形式にして返す std::pair< double,std::vector<Info> > get_best_tree(size_t N, DPTable<Info>& dp){ std::vector<Info> ret; if(N==0 || !dp.exists(0,N-1,grammars.get_start())) return std::make_pair(-1,ret); //開始記号から構文木をたどる size_t i = 0; Info tmp = dp.get(0,N-1,grammars.get_start()); double p = tmp.delta; ret.push_back(tmp); ret[i].ans = std::make_pair(ret.size(), ret.size()+1); ret.push_back(dp.get(tmp.idx.first.first,tmp.idx.first.second,tmp.rhs.first)); ret.push_back(dp.get(tmp.idx.second.first,tmp.idx.second.second,tmp.rhs.second)); i++; while(i < ret.size()){ tmp = ret[i]; if(tmp.rhs.second != ""){ //A -> B C ret[i].ans = std::make_pair(ret.size(), ret.size()+1); ret.push_back(dp.get(tmp.idx.first.first,tmp.idx.first.second,tmp.rhs.first)); //B ret.push_back(dp.get(tmp.idx.second.first,tmp.idx.second.second,tmp.rhs.second));//C } else { //A -> a ret[i].ans = std::make_pair(-1, -1); //a } i++; } return std::make_pair(p, ret); } /* Inside-Outsideアルゴリズム用 */ //DPテーブルを作成 void make_dp_table(DPTable<BetaAlpha>& dp, const std::vector<std::string>& text){ std::vector<Grammar> grms = grammars.get_all_grammar(); size_t N = text.size(); //内側確率betaの計算 {//対角要素を更新 for(size_t i=0; i<N; i++){ std::vector<Grammar> v = grammars.search(std::make_pair(text[i],"")); for(size_t j=0; j<v.size(); j++){ dp.set(i, i, v[j].lhs, BetaAlpha(v[j].lp, -INF)); } } } {//残りの部分を更新 for(size_t n=1; n<N; n++){ for(size_t i=0; i<N-n; i++){ std::map< std::string, std::vector<double> > memo; for(size_t k=0; k<grms.size(); k++){ std::vector<double> v; for(size_t j=1; j<=n; j++){ bool ok = true; //A->B CでBとCが両方0以上の値が存在しているものだけ計算 double lp = 0; if(dp.exists(i,i+j-1,grms[k].rhs.first)){ lp += dp.get(i,i+j-1,grms[k].rhs.first).beta; }else{ ok = false; } if(dp.exists(i+j,i+n,grms[k].rhs.second)){ lp += dp.get(i+j,i+n,grms[k].rhs.second).beta; }else{ ok = false; } if(ok) v.push_back(lp); } if(v.size() > 0) memo[grms[k].lhs].push_back(grms[k].lp + logsumexp(v)); } for(std::map< std::string, std::vector<double> >::iterator itr = memo.begin(); itr != memo.end(); ++itr){ if((itr->second).size() > 0) dp.set(i,i+n,itr->first,BetaAlpha(logsumexp(itr->second), -INF)); } } } } if(!dp.exists(0,N-1,grammars.get_start())) return; //構築に失敗したら終了 //外側確率alphaの計算 {//一番右上の外側確率を設定 BetaAlpha ba = dp.get(0,N-1,grammars.get_start()); dp.set(0,N-1,grammars.get_start(),BetaAlpha(ba.beta,0)); } {//A -> B Cの形の生成規則に対し、Aの外側確率からBとCの外側確率を更新 for(size_t n=N-1; n>=1; n--){ for(size_t i=0; i<N-n; i++){ for(size_t j=0; j<grms.size(); j++){ if(!dp.exists(i,i+n,grms[j].lhs)) continue; std::map< std::pair< std::pair<size_t,size_t>,std::string >, std::vector<double> > memo; for(size_t k=1; k<=n; k++){ //alpha[i+k][i+n][C] += P(A->BC) * alpha[i][i+n][A] * beta[i][i-1+k][B] if(dp.exists(i+k,i+n,grms[j].rhs.second) && dp.exists(i,i-1+k,grms[j].rhs.first)){ double lp = grms[j].lp + dp.get(i,i+n,grms[j].lhs).alpha + dp.get(i,i-1+k,grms[j].rhs.first).beta; memo[std::make_pair(std::make_pair(i+k,i+n),grms[j].rhs.second)].push_back(lp); } //alpha[i][i+n-k][B] += P(A->BC) * alpha[i][i+n][A] * beta[i+n+1-k][i+n][C] if(dp.exists(i,i+n-k,grms[j].rhs.first) && dp.exists(i+n+1-k,i+n,grms[j].rhs.second)){ double lp = grms[j].lp + dp.get(i,i+n,grms[j].lhs).alpha + dp.get(i+n+1-k,i+n,grms[j].rhs.second).beta; memo[std::make_pair(std::make_pair(i,i+n-k),grms[j].rhs.first)].push_back(lp); } } for(std::map< std::pair< std::pair<size_t,size_t>,std::string >, std::vector<double> >::iterator itr = memo.begin(); itr != memo.end(); ++itr){ size_t l = (itr->first).first.first; size_t r = (itr->first).first.second; std::string A = (itr->first).second; if(!dp.exists(l,r,A)) continue; std::vector<double> v = itr->second; BetaAlpha ba = dp.get(l,r,A); v.push_back(ba.alpha); ba.alpha = logsumexp(v); dp.set(l,r,A,ba); } } } } } } //テキストの確率値を取得 double get_sentence_prob(DPTable<BetaAlpha>& dp, const std::vector<std::string>& text){ size_t N = text.size(); return dp.get(0,N-1,grammars.get_start()).beta; } //コーパスの尤度を計算 double calc_log_likelihood(const std::vector< std::vector<std::string> >& corpus){ double ret = 0.0; for(size_t i=0; i<corpus.size(); i++){ DPTable<BetaAlpha> dp(corpus[i].size()); make_dp_table(dp, corpus[i]); if(!dp.exists(0,corpus[i].size()-1,grammars.get_start())){ //構文木が作成できていない場合はスキップ //std::cerr << "text[" << i << "] skipped" << std::endl; continue; } double lp = get_sentence_prob(dp, corpus[i]); //std::cerr << "text[" << i << "] = " << lp << std::endl; ret += lp; } return ret; } //ルールの適用確率の推定 void update_grammar_prob(const std::vector< std::vector<std::string> >& corpus){ std::vector<Grammar> grms = grammars.get_all_grammar(); std::map< Grammar,std::vector<double> > cnt; //適用された回数をカウント for(size_t t=0; t<corpus.size(); t++){ size_t N = corpus[t].size(); DPTable<BetaAlpha> dp(N); make_dp_table(dp, corpus[t]); if(!dp.exists(0,N-1,grammars.get_start())) continue; //構文木が作成できていない場合はスキップ double lp_sentence = get_sentence_prob(dp, corpus[t]); for(size_t g=0; g<grms.size(); g++){ std::vector<double> v; if(grms[g].rhs.second == ""){ //A -> a for(size_t i=0; i<N; i++){ if(dp.exists(i,i,grms[g].lhs)) v.push_back(grms[g].lp - lp_sentence + dp.get(i,i,grms[g].lhs).alpha); } }else{ //A -> B C for(size_t n=1; n<=N-1; n++){ for(size_t i=0; i<N-n; i++){ for(size_t j=1; j<=n; j++){ if(!dp.exists(i,i+n,grms[g].lhs)) continue; if(!dp.exists(i,i+j-1,grms[g].rhs.first)) continue; if(!dp.exists(i+j,i+n,grms[g].rhs.second)) continue; double lp = grms[g].lp - lp_sentence + dp.get(i,i+n,grms[g].lhs).alpha + dp.get(i,i+j-1,grms[g].rhs.first).beta + dp.get(i+j,i+n,grms[g].rhs.second).beta; v.push_back(lp); } } } } cnt[grms[g]].push_back(logsumexp(v)); } } //適用回数から確率を計算し、grammarsを更新 std::map< std::string,std::vector<double> > sum; for(std::map< Grammar,std::vector<double> >::iterator itr = cnt.begin(); itr != cnt.end(); ++itr){ sum[(itr->first).lhs].push_back(logsumexp(itr->second)); } Grammars new_grms; new_grms.set_start(grammars.get_start()); for(size_t i=0; i<grms.size(); i++){ double lp = logsumexp(cnt[grms[i]]) - logsumexp(sum[grms[i].lhs]); new_grms.add(Grammar(grms[i].lhs, grms[i].rhs, lp)); } grammars = new_grms; } public: //文法の開始記号を登録 void set_start(const std::string& st){ grammars.set_start(st); } //文法を登録 void add_grammar(const std::string& lhs, const std::pair<std::string,std::string>& rhs, double lp){ grammars.add(Grammar(lhs,rhs,lp)); } //文に対して最尤な導出を計算 std::pair< double, std::vector<Info> > calc_best_tree(const std::vector<std::string>& text){ size_t N = text.size(); DPTable<Info> dp(N); //対角要素を計算 for(size_t i=0; i<N; i++){ std::vector<Grammar> v = grammars.search(std::make_pair(text[i],"")); for(size_t j=0; j<v.size(); j++){ Info info; info.lhs = v[j].lhs; info.rhs = v[j].rhs; info.idx.first = std::make_pair(i,i); info.idx.second = std::make_pair(-1,-1); info.delta = v[j].lp; if(dp.get(i, i, v[j].lhs).delta < v[j].lp){ dp.set(i, i, v[j].lhs, info); } } } //三角行列の2番目以降の対角線上の要素を計算 for(size_t n=1; n<N; n++){ for(size_t i=0; i<N-n; i++){ for(size_t j=1; j<=n; j++){ std::vector<std::string> v1 = dp.get_str_list(i, i+j-1); std::vector<std::string> v2 = dp.get_str_list(i+j, i+n); for(size_t v1i=0; v1i<v1.size(); v1i++){ for(size_t v2i=0; v2i<v2.size(); v2i++){ std::vector<Grammar> v = grammars.search(std::make_pair(v1[v1i],v2[v2i])); for(size_t k=0; k<v.size(); k++){ if(dp.get(i, i+n, v[k].lhs).delta < v[k].lp + dp.get(i,i+j-1,v1[v1i]).delta + dp.get(i+j,i+n,v2[v2i]).delta){ Info info; info.lhs = v[k].lhs; info.rhs = v[k].rhs; info.idx.first = std::make_pair(i,i+j-1); info.idx.second = std::make_pair(i+j,i+n); info.delta = v[k].lp + dp.get(i,i+j-1,v1[v1i]).delta + dp.get(i+j,i+n,v2[v2i]).delta; dp.set(i,i+n,v[k].lhs,info); } } } } } } } return get_best_tree(N, dp); } //Inside-Outside algorithmで文法の確率値を推定 void estimate(const std::vector< std::vector<std::string> >& corpus, size_t ITER = 100000, double EPS = 1e-6){ std::cerr << "Start Training..." << std::endl; //文法の確率を適当な値で埋める grammars.fill_random(); double LL_prev = -INF, LL_now; for(size_t iter=1; iter<=ITER; iter++){ //確率値の更新 update_grammar_prob(corpus); //尤度の計算 LL_now = calc_log_likelihood(corpus); std::cerr << "ITER = " << iter << "\tLL : " << LL_now << std::endl; if(fabs(LL_now - LL_prev) < EPS) break; LL_prev = LL_now; } //推定後の文法情報をダンプ std::cout << "[New Grammar]" << std::endl; grammars.dump(); std::cout << std::endl; } //文を解析し、結果を出力、文の確率を返す double dump(const std::vector<std::string>& text){ size_t N = text.size(); std::pair< double, std::vector<Info> > best_tree = calc_best_tree(text); std::vector<Info> ret = best_tree.second; DPTable<BetaAlpha> dp(N); make_dp_table(dp, text); double lp_sentence = 0.0; if(dp.exists(0,N-1,grammars.get_start())){ lp_sentence = get_sentence_prob(dp, text); } std::cout << "Text : "; for(size_t i=0; i<text.size(); i++){ if(i!=0) std::cout << " "; std::cout << text[i]; } std::cout << std::endl; std::cout << "P(W,T_best) : " << exp(best_tree.first) << std::endl; std::cout << "P(W) : " << exp(lp_sentence) << std::endl; for(size_t i=0; i<best_tree.second.size(); i++){ std::cout << i << "\t"; std::cout << ret[i].ans.first << "\t" << ret[i].ans.second << "\t"; std::cout << ret[i].lhs << " -> " << ret[i].rhs.first << " " << ret[i].rhs.second << std::endl; } std::cout << std::endl; return best_tree.first; } }; const double PCFG::INF = 1e100; int main(){ PCFG pcfg; //文法の登録(書籍のp.128図5.1) pcfg.set_start("S"); //開始記号 pcfg.add_grammar("S", std::make_pair("N","V"), log(0.4)); pcfg.add_grammar("S", std::make_pair("S","PP"), log(0.5)); pcfg.add_grammar("S", std::make_pair("V","N"), log(0.1)); pcfg.add_grammar("V", std::make_pair("V","N"), log(0.4)); pcfg.add_grammar("PP", std::make_pair("P","N"), log(1.0)); pcfg.add_grammar("N", std::make_pair("N","PP"), log(0.1)); pcfg.add_grammar("N", std::make_pair("I",""), log(0.4)); pcfg.add_grammar("N", std::make_pair("Maria",""), log(0.3)); pcfg.add_grammar("N", std::make_pair("pizza",""), log(0.2)); pcfg.add_grammar("V", std::make_pair("eat",""), log(0.6)); pcfg.add_grammar("P", std::make_pair("with",""), log(1.0)); //コーパス std::vector< std::vector<std::string> > corpus; { //I eat pizza with Maria std::vector<std::string> text; text.push_back("I"); text.push_back("eat"); text.push_back("pizza"); text.push_back("with"); text.push_back("Maria"); corpus.push_back(text); } { //Maria eats pizza std::vector<std::string> text; text.push_back("Maria"); text.push_back("eat"); text.push_back("pizza"); corpus.push_back(text); } //コーパス全体の対数尤度の合計 double ll_sum; //指定した確率値での解析結果 ll_sum = 0; for(size_t i=0; i<corpus.size(); i++){ ll_sum += pcfg.dump(corpus[i]); } std::cout << "LLsum = " << ll_sum << std::endl; std::cout << std::endl; //適用確率を推定 pcfg.estimate(corpus); //推定後の確率値での解析結果 ll_sum = 0; for(size_t i=0; i<corpus.size(); i++){ ll_sum += pcfg.dump(corpus[i]); } std::cout << "LLsum = " << ll_sum << std::endl; std::cout << std::endl; return 0; }
結果
実行結果。
導出木の配列の部分は、以下の形式。
木のノード番号(0は根ノード) 左の子ノードの番号 右の子ノードの番号 適用規則
Text : I eat pizza with Maria P(W,T_best) : 0.001152 //書籍のp.128 P(W,T_2)と同じ P(W) : 0.0013824 //書籍のp.129 P(W)と同じ 0 1 2 S -> S PP 1 3 4 S -> N V 2 5 6 PP -> P N 3 -1 -1 N -> I 4 7 8 V -> V N 5 -1 -1 P -> with 6 -1 -1 N -> Maria 7 -1 -1 V -> eat 8 -1 -1 N -> pizza Text : Maria eat pizza P(W,T_best) : 0.00576 P(W) : 0.00576 0 1 2 S -> N V 1 -1 -1 N -> Maria 2 3 4 V -> V N 3 -1 -1 V -> eat 4 -1 -1 N -> pizza LLsum = -11.9231 Start Training... ITER = 1 LL : -11.9597 ITER = 2 LL : -11.7674 ITER = 3 LL : -11.7563 ITER = 4 LL : -11.7553 ITER = 5 LL : -11.7552 ITER = 6 LL : -11.7552 ITER = 7 LL : -11.7552 ITER = 8 LL : -11.7552 [New Grammar] N -> I 0.532391 N -> Maria 0.355308 N -> N PP 1.2904e-08 S -> N V 0.666667 PP -> P N 1 S -> S PP 0.333333 S -> V N 0 V -> V N 0.5 V -> eat 0.5 N -> pizza 0.112301 P -> with 1 Text : I eat pizza with Maria P(W,T_best) : 0.00118018 P(W) : 0.00118018 0 1 2 S -> S PP 1 3 4 S -> N V 2 5 6 PP -> P N 3 -1 -1 N -> I 4 7 8 V -> V N 5 -1 -1 P -> with 6 -1 -1 N -> Maria 7 -1 -1 V -> eat 8 -1 -1 N -> pizza Text : Maria eat pizza P(W,T_best) : 0.00665024 P(W) : 0.00665024 0 1 2 S -> N V 1 -1 -1 N -> Maria 2 3 4 V -> V N 3 -1 -1 V -> eat 4 -1 -1 N -> pizza LLsum = -11.7552
ランダムな確率から(toy)コーパスを使って推定しなおしても構文木は同じ結果になっている。
1つ目の文の構文木は以下。

上記の推定では、コーパスに出現してない生成規則「N -> N PP」の確率値が小さくなって、推定規則を使ったコーパスの対数尤度が元の対数尤度より大きくすることができている模様(-11.9231→-11.7552)。
また、初期値に与える確率値を変えると結果も変わることも確認できる。(EMアルゴリズム的に)
参考
- 北, 言語と計算4 確率的言語モデル, 東京大学出版会
- https://www.cs.jhu.edu/~jason/465/iobasics.pdf
FastBDTでの高速化
はじめに
勾配ブースティング木の高速化はどうすればいいだろうと調べていたら、arxivで流れているのを見かけたのでメモ。
- FastBDT: A speed-optimized and cache-friendly implementation of stochastic gradient-boosted decision trees for multivariate classification
Stochastic Gradient Boosted Decision Tree(SGBDT)
- 勾配ブースティングの各イテレーションで、学習データから非復元抽出でサンプリングしたデータを用いる
- https://statweb.stanford.edu/~jhf/ftp/stobst.pdf
- 「統計的学習の基礎 データマイニング・推論・予測(共立出版)」だと、Importance sampled learning ensemble(ISLE)あたり?
- https://www.rco.recruit.co.jp/career/engineer/blog/32/
高速化
メモリアクセス、CPUキャッシュ、前処理、並列化を考慮。
メモリアクセスパターン
- 学習データのメモリ配置について最適化
- 一般的に以下の2つのレイアウト方式が考えられる
- array of structs(構造体の配列) : x_1, y_1, z_1, x_2, y_2, z_2, x_3, y_3, z_3, x_4, y_4, z_4
- struct of arrays(配列の構造体) : x_1, x_2, x_3, x_4, y_1, y_2, y_3, y_4, z_1, z_2, z_3, z_4
- FastBDTは「array of structs」を利用
- CPUキャッシュの空間的局所性(例:linear memory access pattern)、時間的局所性(小さなCPHのキャッシュ)、CPUの分岐局所性(conditional jumpをできるだけ避ける)を考慮
【正例と負例のメモリマップ】
- array of structsを利用する場合、そのまま並べてしまうと、正例と負例の判定で条件分岐が必要になってしまう
- そこで、正例と負例のデータを分けて、保存や処理を行う
【レイヤー毎の複数ノードの処理】
- ノード単位で別々にノードを処理していく方法だと、使用する学習データへのアクセスがとびとびになってしまい、メモリレイアウト方式によらずランダムにジャンプしてアクセスしてしまう
- (DFS的な感じでのノードの処理?)
- 木のレイヤー単位で、そのレイヤーすべてのノードを並列処理することができると、連続的なメモリアクセスにできる
【確率的サブサンプリング】
- SGBDTだと、学習データからサンプリングしたデータを使用するため、使うデータと使わないデータを選ぶ必要がある
- array of structsだと、各データポイントの範囲内であれば、条件分岐なしでデータへ連続的にアクセスできる
前処理
勾配ブースティング木を試す
はじめに
ここしばらくサボってしまっているので、(のんびりと)いろいろ勉強していきたい。
コンテスト系などでもよい成績を残している勾配ブースティング木について試してみた。
勾配ブースティングとは
- Gradient Boosting
- 加法的モデルH(x)=Σρ_t * h_t(x)を、前向き段階的に各ρ,hを学習・追加していく
- h_tは弱学習器、ρ_tは弱学習器tの貢献度
- 雑に言うと、tでは(t-1)まででの予測の弱点を補うような弱学習器h_tを学習・追加する
- 弱点は「予測結果と正解との差」が考えられるが、差ではなく(負の)勾配として考える
- なんらかの損失関数を定めることで、その勾配を弱学習器h_tに学習させていく(勾配降下している感じ)
- ρ_tは学習率に相当
- 勾配ブースティング木は、弱学習器として決定木・回帰木を用いたもの
- 多重加法的回帰木(multiple additive regression trees)とも
損失関数と負の勾配
- Square Loss
- loss = 1/2 * { y_i - H(x_i) }^2
- -grad = y_i - H(x_i)
- 「正解と予測値の差」を学習していく
- Absolute Loss
- loss = |y_i - H(x_i)|
- -grad = sign(y_i - H(x_i))
- Huber Loss
ライブラリ
実用で使う場合は、以下のような有用なライブラリがあるので、そちらを使うのがよい。
- https://github.com/dmlc/xgboost
- python sklearn.ensemble
- とか
コード
毎度ながら、アルゴリズムを追いたいので、工夫や効率化などはしてない。
回帰木は、木の深さを指定し、そこまでノードを増やす(作れない場合はそこまで)。
変数の探索は、全データ全変数を探すので重い。
#include <iostream> #include <vector> #include <fstream> //回帰木 class RT { struct NODE { int ln, rn; //左のノードID、右のノードID int j; //分割変数 double th; //分割閾値 std::vector<int> ids; //割り当てられた学習データのID double ybar; //平均値 NODE():ln(-1),rn(-1),j(-1),th(0),ybar(0){} }; int N; //木のノード数 int depth; //木の深さ std::vector<NODE> nodes; //木のノード情報 const double INF; //分割関数 double split_value(int j, double th, int id, const std::vector< std::vector<double> >& x, const std::vector<double>& y){ //分割したときのそれぞれのyの平均値 double lybar = 0.0, rybar = 0.0; int lnum = 0, rnum = 0; for(size_t i=0; i<nodes[id].ids.size(); i++){ int ii = nodes[id].ids[i]; if(x[ii][j] < th){ lybar += y[ii]; lnum++; }else{ rybar += y[ii]; rnum++; } } if(lnum == 0 || rnum == 0) return INF; lybar /= lnum; rybar /= rnum; //それぞれの二乗和を求める double lcost = 0.0, rcost = 0.0; for(size_t i=0; i<nodes[id].ids.size(); i++){ int ii = nodes[id].ids[i]; if(x[ii][j] < th){ lcost += (y[ii] - lybar) * (y[ii] - lybar); }else{ rcost += (y[ii] - rybar) * (y[ii] - rybar); } } //二乗和の合計を最小化の基準にする return lcost + rcost; } //ノードidにおける最適な分割基準を見つける std::pair<int, double> search_best_split(int id, const std::vector< std::vector<double> >& x, const std::vector<double>& y){ std::pair<int, double> best(-1, INF); double best_value = INF; int dim = x[0].size(); for(int j=0; j<dim; j++){ //閾値候補 std::vector<double> v; for(size_t i=0; i<nodes[id].ids.size(); i++){ v.push_back(x[nodes[id].ids[i]][j]); } //変数jと閾値v[i]で分割したときの分割関数の値を計算 for(size_t i=0; i<v.size(); i++){ double res = split_value(j, v[i], id, x, y); if(best_value > res){ best_value = res; best.first = j; best.second = v[i]; } } } return best; } //木を成長させる void grow_tree(int id, const std::vector< std::vector<double> >& x, const std::vector<double>& y){ //ノードに割り当てられた学習データのyの平均値 nodes[id].ybar = 0.0; for(size_t i=0; i<nodes[id].ids.size(); i++){ nodes[id].ybar += y[nodes[id].ids[i]]; } if(nodes[id].ids.size() == 0) return; nodes[id].ybar /= nodes[id].ids.size(); //子ノードを準備 if(2*id + 1 >= N) return; nodes[id].ln = 2*id + 1; nodes[id].rn = 2*id + 2; //最適な分割変数、分割閾値を探索 std::pair<int, double> best = search_best_split(id, x, y); nodes[id].j = best.first; nodes[id].th = best.second; if(best.first == -1) return; //子ノードに学習データを分類する for(size_t i=0; i<nodes[id].ids.size(); i++){ if(x[nodes[id].ids[i]][nodes[id].j] < nodes[id].th){ //閾値未満なら左ノードへ nodes[nodes[id].ln].ids.push_back(nodes[id].ids[i]); }else{ //閾値以上なら右ノードへ nodes[nodes[id].rn].ids.push_back(nodes[id].ids[i]); } } std::vector<int>(nodes[nodes[id].ln].ids).swap(nodes[nodes[id].ln].ids); std::vector<int>(nodes[nodes[id].rn].ids).swap(nodes[nodes[id].rn].ids); } public: RT(int depth_):depth(depth_),INF(1e23){ N = (1<<depth) - 1; } void fit(const std::vector< std::vector<double> >& x, const std::vector<double>& y){ //木の初期化 nodes.clear(); nodes.resize(N); for(int i=0; i<static_cast<int>(y.size()); i++){ nodes[0].ids.push_back(i); } std::vector<int>(nodes[0].ids).swap(nodes[0].ids); //木を成長させる for(int i=0; i<N; i++){ grow_tree(i, x, y); } //木の各ノードの不要な情報を削除 for(int i=0; i<N; i++) nodes[i].ids.clear(); } double predict(const std::vector<double>& x){ if(N == 0) return 0; int id = 0; while(true){ if(nodes[id].j == -1) return nodes[id].ybar; if(x[nodes[id].j] < nodes[id].th) id = nodes[id].ln; else id = nodes[id].rn; } } }; //勾配ブースティング木 class GradientBoostingTree { static const int treedepth = 3; int iter; std::vector<RT> trees; double rho; //学習率 //勾配を計算 double calc_ngrad(double y, double f){ //Square loss return y - f; //Absolute loss //return (y-f>0?1:-1); //Huber loss //double delta = 1.0; //if(fabs(y-f) < delta) return y - f; //else return (delta * (y-f>0?1:-1)); } public: GradientBoostingTree(int iter, double rho = 1.0): iter(iter),trees(iter, RT(treedepth)),rho(rho){ } void fit(const std::vector< std::vector<double> >& x, const std::vector<double>& y){ //最初に普通にtree[0]をfit trees[0].fit(x, y); //現在までの計算結果をfに保存 std::vector<double> f(y.size()); for(size_t i=0; i<y.size(); i++){ f[i] = trees[0].predict(x[i]); } //(iter-1)回勾配降下する for(int i=1; i<iter; i++){ //負の勾配を計算 std::vector<double> ngrad(y.size(), 0.0); for(size_t j=1; j<ngrad.size(); j++){ ngrad[j] = calc_ngrad(y[j], f[j]); } //tree[i]でfit trees[i].fit(x, ngrad); //fit後の予測値で値を更新 for(size_t j=0; j<y.size(); j++){ f[j] += rho * trees[i].predict(x[j]); } } } double predict(const std::vector<double>& x){ double ret = trees[0].predict(x); for(int i=1; i<iter; i++){ ret += rho * trees[i].predict(x); } return ret; } }; int main(int argc, char** argv){ std::vector< std::vector<double> > train_x, test_x; std::vector<double> train_y, test_y; {//学習データの読み込み std::ifstream trainfs(argv[1]); int dim; trainfs >> dim; double x, y; while(trainfs >> y){ train_y.push_back(y); std::vector<double> tmp; for(int i=0; i<dim; i++){ trainfs >> x; tmp.push_back(x); } train_x.push_back(tmp); } } std::cerr << "load file : " << argv[2] << std::endl; {//テストデータの読み込み std::ifstream testfs(argv[2]); int dim; testfs >> dim; double x, y; while(testfs >> y){ test_y.push_back(y); std::vector<double> tmp; for(int i=0; i<dim; i++){ testfs >> x; tmp.push_back(x); } test_x.push_back(tmp); } } std::cerr << "done..." << std::endl; //学習 GradientBoostingTree rt(100, 0.5); std::cerr << "fitting..." << std::endl; rt.fit(train_x, train_y); std::cerr << "done..." << std::endl; //予測 std::cout << "#test_y\tpredict" << std::endl; for(size_t i=0; i<test_y.size(); i++){ std::cout << test_y[i] << "\t" << rt.predict(test_x[i]) << std::endl; } return 0; }
実験
データ
https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/regression.html#eunite2001
libsvmのregressionデータの「eunite2001」の学習データとテストデータを使ってみてみる。
データの形式
入力の形式は、
次元 y_t x_1 x_2 x_3 ... ...
のように変換して入力。
$ cat ./data/eunite2001.in 16 818.0 0 0 1 0 0 0 0 0 0 0.859223 0.645631 0.589806 0.711165 0.808252 0.759709 0.808252 803.0 0 0 0 1 0 0 0 0 0 0.859223 0.859223 0.645631 0.589806 0.711165 0.808252 0.759709 804.0 0 0 0 0 1 0 0 0 0 0.822816 0.859223 0.859223 0.645631 0.589806 0.711165 0.808252 746.0 0 0 0 0 0 1 0 0 0 0.825243 0.822816 0.859223 0.859223 0.645631 0.589806 0.711165 730.0 0 0 0 0 0 0 0 0 0 0.684466 0.825243 0.822816 0.859223 0.859223 0.645631 0.589806 ...
参考文献
- T. Hastieら, 統計的学習の基礎 データマイニング・推論・予測, 共立出版
- K. P. Murphy, Machine Learning -A Probabilistic Perspective-
- https://statweb.stanford.edu/~jhf/ftp/trebst.pdf
- https://en.wikipedia.org/wiki/Gradient_boosting
- http://www.ccs.neu.edu/home/vip/teach/MLcourse/4_boosting/slides/gradient_boosting.pdf
t-SNEで遊ぶ
はじめに
最近よく見かける「t-SNE」という非線形次元圧縮手法を試してみた。
t-SNEとは
- t-Distributed Stochastic Neighbor Embedding
- SNEと呼ばれる次元圧縮手法の問題点を改善した手法
- 低次元での分布に「自由度1のt-分布」を利用する
- さらに、高速化を行った「Barnes-Hut t-SNE」という手法ではO(n log n)で計算できる
詳しい説明は、元論文や紹介記事がたくさんある。
- https://lvdmaaten.github.io/publications/papers/JMLR_2008.pdf
- http://www.slideshare.net/t_koshikawa/visualizing-data-using-tsne-56773191
- http://blog.albert2005.co.jp/2015/12/02/tsne/
- http://puyokw.hatenablog.com/entry/2015/06/21/000102
また、実用で使う場合は、以下に各種実装へのリンクがまとめられているので、そちらを使うのがよい。
https://lvdmaaten.github.io/tsne/
コード
元論文にある「Algorithm 1: Simple version of t-Distributed Stochastic Neighbor Embedding」をそのまま実装したつもり。
論文で紹介されている「early compression」「early exaggeration」はいれていない。
#include <iostream> #include <vector> #include <cmath> // 注意: longではなくint(32bit)にすべき unsigned long xor128(){ static unsigned long x=123456789, y=362436069, z=521288629, w=88675123; unsigned long t; t=(x^(x<<11)); x=y; y=z; z=w; return w=(w^(w>>19))^(t^(t>>8)); } // 注意: int_maxぐらいで割るべき double frand(){ return xor128()%1000000/static_cast<double>(1000000); } static const double PI = 3.14159265358979323846264338; double normal_rand(double mu, double sigma2){ double sigma = sqrt(sigma2); double u1 = frand(), u2 = frand(); double z1 = sqrt(-2*log(u1)) * cos(2*PI*u2); //double z2 = sqrt(-2*log(u1)) * sin(2*PI*u2); return mu + sigma*z1; } typedef std::vector<double> P; static const double EPS = 1e-5; class tSNE { int fromDim, toDim; double perp; int T; double eta; double dist2(const P& xi, const P& xj){ double ret = 0.0; for(int i=0; i<xi.size(); i++){ ret += (xi[i]-xj[i]) * (xi[i]-xj[i]); } return ret; } public: tSNE(int fromDim, int toDim = 2, double perp = 5.0, int T = 100000, double eta = 100): fromDim(fromDim), toDim(toDim), perp(perp), T(T), eta(eta) { } std::vector<P> reduce(const std::vector<P>& X){ int N = X.size(); std::vector<P> Y(N, P(toDim,0)); //compute pairwise affinities p(j|i) with perplexity perp std::vector< std::vector<double> > condP(N, std::vector<double>(N,0)); for(int i=0; i<N; i++){ //binary search double lb = 0.0, ub = 1e10; for(int bi=0; bi<200; bi++){ double sigma2 = (lb+ub)/2.0; for(int j=0; j<N; j++){ if(i!=j){ condP[j][i] = exp( -dist2(X[i],X[j]) / (2.0 * sigma2) ); }else{ condP[j][i] = 0.0; } } double sum = 0.0; for(int k=0; k<N; k++){ if(i != k) sum += condP[k][i]; } for(int j=0; j<N; j++){ condP[j][i] /= sum; } //compute perplexity double HPi = 0.0; for(int j=0; j<N; j++){ if(i!=j) HPi -= condP[j][i] * log(condP[j][i]); } double perpPi = pow(2.0, HPi); if(perpPi < perp) lb = sigma2; else ub = sigma2; } std::cerr << "sigma^2 of " << i << " = " << lb << std::endl; } //set p(i,j) std::vector< std::vector<double> > jointP(N, std::vector<double>(N,0)); for(int i=0; i<N; i++){ for(int j=0; j<N; j++){ if(i!=j) jointP[i][j] = (condP[j][i] + condP[i][j]) / (2.0 * N); } } //sample initial solution Y^(0) for(int i=0; i<N; i++){ for(int j=0; j<toDim; j++){ Y[i][j] = normal_rand(0.0, 0.001); } } //iteration std::vector<P> diff(N, P(toDim, 0)); double alpha = 0.5; for(int t=1; t<=T; t++){ std::vector<P> newY = Y; //compute low-dimensional affinities q(i,j) std::vector< std::vector<double> > jointQ(N, std::vector<double>(N,0)); double sum = 0.0; for(int k=0; k<N; k++){ for(int l=0; l<N; l++){ if(k!=l) sum += 1.0 / (1.0 + dist2(Y[k], Y[l])); } } for(int i=0; i<N; i++){ for(int j=0; j<N; j++){ if(i!=j){ jointQ[i][j] = 1.0 / (1.0 + dist2(Y[i], Y[j])); jointQ[i][j] /= sum; } } } //(compute cost C = KL(P||Q)) double cost = 0.0; for(int i=0; i<N; i++){ for(int j=0; j<N; j++){ if(i!=j){ cost += jointP[i][j] * log( jointP[i][j] / jointQ[i][j] ); } } } //compute gradient std::vector<P> delta(N, P(toDim, 0)); for(int i=0; i<N; i++){ for(int j=0; j<N; j++){ if(i!=j){ double a = (jointP[i][j] - jointQ[i][j]) * (1.0 / (1.0 + dist2(Y[i], Y[j]))); for(int k=0; k<toDim; k++){ delta[i][k] += 4.0 * a * (Y[i][k] - Y[j][k]); } } } } //set Y^(t) for(int i=0; i<N; i++){ for(int j=0; j<toDim; j++){ newY[i][j] = Y[i][j] - eta * delta[i][j] + alpha * diff[i][j]; diff[i][j] = newY[i][j] - Y[i][j]; } } Y = newY; if(t%100==0){ std::cerr << "t = " << t << " : cost = " << cost << std::endl; } if(t >= 250) alpha = 0.8; } return Y; } }; int main(){ int N, fromDim, toDim; std::cin >> N; std::cin >> fromDim >> toDim; //input std::vector<P> X; for(int i=0; i<N; i++){ P p(fromDim, 0); for(int j=0; j<fromDim; j++){ std::cin >> p[j]; } X.push_back(p); } //compute tSNE tsne(fromDim, toDim, 5.0, 100000, 100.0); std::vector<P> Y = tsne.reduce(X); //output for(int i=0; i<N; i++){ for(int j=0; j<toDim; j++){ if(j!=0) std::cout << "\t"; std::cout << Y[i][j]; } std::cout << std::endl; } return 0; }
実験
MNISTの「test」のデータから500件分をプロット。各要素は0〜255だったようなので、256で割った値を入力として利用。
入力の形式は、
データ点数 高次元での次元数 低次元での次元数 高次元でのデータ点1(タブかスペース区切り、高次元での次元数分) 高次元でのデータ点2(タブかスペース区切り、高次元での次元数分) ...
にしている。
$ cat in.txt 500 784 2 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 ... ...
ステップ5000ずつの低次元マッピングの状態をプロットしてみる。mnistの数字(0〜9)ごとに色や記号の形をわけている。

最初のバラバラな状態からすぐに塊ができて、それらが微調整されていっている。
効率化テクニックを入れていないせいか、どんどん大きくなっているし、10万回回してもまだ収束しきっていないようにも見える。。。
参考文献
- https://en.wikipedia.org/wiki/T-distributed_stochastic_neighbor_embedding
- http://arxiv.org/abs/1301.3342
- https://lvdmaaten.github.io/publications/papers/JMLR_2008.pdf
- https://lvdmaaten.github.io/publications/papers/JMLR_2014.pdf
- http://www.slideshare.net/t_koshikawa/visualizing-data-using-tsne-56773191
- http://blog.albert2005.co.jp/2015/12/02/tsne/
- http://puyokw.hatenablog.com/entry/2015/06/21/000102
- https://lvdmaaten.github.io/tsne/
検索エンジンの日本語トークナイズメモ
トークナイズ処理
- 「検索クエリ」に対してマッチする「ドキュメント」を高速に検索するためにインデクス(索引)を作成する
- 本の最後の方にある「用語 - ページ」のような感じで、速く目的の用語が書いてあるページを調べられる
- インデクスは、日本語の場合文字が連続しているため、「形態素」や「(文字)N-gram」などが使われる
文1「六本木ヒルズに行った」 文2「青山さんから電話があった」 【形態素でインデクスを作成する場合の例】 文1:「六本木ヒルズ」「に」「行く」「た」 文2:「青山」「さん」「から」「電話」「が」「あっ」「た」 【文字2-gram(bigram)でインデクスを作成する場合】 文1:「六本」「本木」「木ヒ」「ヒル」「ルズ」「ズに」「に行」「行っ」「った」 文2:「青山」「山さ」「さん」「んか」「から」「ら電」「電話」「話が」「があ」「あっ」「った」
- 「転置インデクス」はこれを逆にしたもので、以下のように保持することで、そのインデクスを持つ文を高速に探せる
六本木ヒルズ:文1 青山:文2 た:文1、文2 ...
トークナイズ処理における問題
- 「六本木ヒルズ」というインデクスを作ってしまうと、検索クエリで「ヒルズ」が来た場合、転置インデクス内には完全マッチするものはないので、検索できず検索漏れになる
- なので、できるだけ短めの単位でインデクスが作られている方がよかったりするが、短くすると意味が違ってしまうものまで拾ってしまう可能性がでてくる
- また、検索クエリ側でもインデクスと同じ処理をし単位をそろえる必要があるが、形態素解析などを使うと「クエリの解析結果」と「文章中での解析結果」がちょっと変わってしまったりすることがある
- 高橋,颯々野,「情報検索のための単語分割一貫性の定量的評価」,NLP2016
- http://research-lab.yahoo.co.jp/nlp/20160307_ftakahas.html
- カタカナ、アルファベット、数字、記号などは、日本語の形態素解析ではきちんと解析されない場合、それらを含む検索に失敗する可能性もある
- 字種交じりだと切れ目がおかしくなりやすい
基本処理・工夫
形態素+N-gramでのハイブリットインデクシング
http://www.slideshare.net/techblogyahoo/17lucenesolr-solrjp-apache-lucene-solrnbest
辞書登録による解析単位の調整
同上
- 短い単位に解析されるよう辞書に登録
- 登録するのが大変(保守も大変)
kuromojiのSEARCH MODE
品詞や文字の正規化・除外・ストップワード
http://www.rondhuit.com/solr%E3%81%AE%E6%97%A5%E6%9C%AC%E8%AA%9E%E5%AF%BE%E5%BF%9C.html
トークンの部分一致検索
- (長めの)形態素の部分文字列を高速に検索できるようにしておくことで、検索ヒット数が少ない場合の検索再現率を改善
- 形態素(トークン)に対して、半無限文字列(i文字目から最後の文字までの部分文字列)を前方一致で検索
- suffix array的な感じ。パトレシアトライなどを使っている模様
表記ゆれ、同義語の考慮
同上
- 表記が「サーバー」「サーバ」や「バイオリン」「ヴァイオリン」など揺れる可能性がある
- これらを同一視できるような辞書を用意して統一しておく