特異値分解
(一般)
【とくいちぶんかい】
SVD (singular value decomposition)
線形代数の行列分解の一手法。統計学や信号処理で活用されている。
特異値分解定理
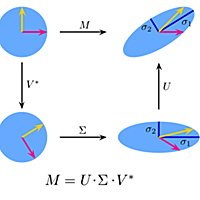
特異値分解定理によれば、m行n列の行列Mは
M = U Σ V*
の形に分解する事ができる。
U : 行列Mの入力の基底となる正規直交ベクトル (m次ユニタリ行列)
V : 行列Mの出力の基底となる正規直交ベクトル (n次ユニタリ行列)
要するに特異値分解とは、入力と出力の線形関係Mを、正規直交化して 特異値 Σii を求める処理と言える。
特異値分解による次元削減
行列Mが既約ではない(行または列に従属関係がある)場合、あるいは特異値が極めて0に近い場合、行列Σの次数を下げる事ができ、大きな行列の次数削減に利用される。
また、行列の次数が極めて大きく計算機のメモリーにも収まらない場合には、
逐次計算可能なアルゴリズムや、ニューラルネットを使ったアルゴリズムが試みられている。