双代数法則

双代数法則（双代数条件）とは、1つの圏にデカルト構造、余デカルト構造が載っているとき、それらが協調していることを示す条件である。∇;Δ = □ という等式で示せる。

双代数法則は、対角Δがモノイド射（加法的）であること、また、加法∇がコモノイド射（余加法的）であることを主張している。このことは、行列の絵算で容易に確認できる。

双代数法則を絵算で使うとき、位相的同位変形ではなくて、ある領域（チャンバー、ボックス）を置換することになる。これは2次元で計算（絵の変形）しているせいで、3次元なら特異点を通る変形、4次元ならおそらく特異性が表れない変形となるだろう。

絵算の外部空間（背景）の次元が低いと、同値変形で特異性が出現する。加法の交換法則やヤンキングを2次元内で遂行しようとすると、特異性が避けられない。

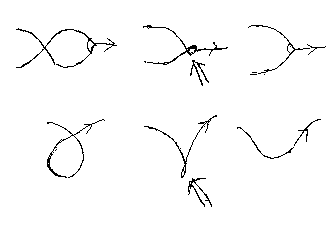
3次元を使って変形すれば、特異性は出ないが、2次元では変形の途中で捻れやシコリ、ダマを無理に潰すことになる。

さて、双代数法則を3次元内で表現すると次のようになる。

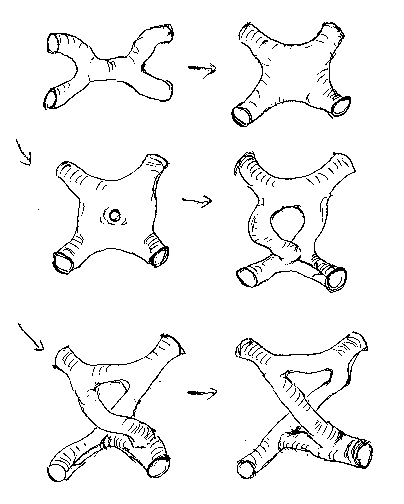
4つの穴が開いた球面が、4つの穴が開いたトーラスに変わる瞬間がある。そこが変形の特異点になっている。その他は連続変形である。