id:hiroki_fさんが、気合いで書いた解説があるので、予備知識の説明はそちらをどうぞ。僕は、もっと泥臭い計算(elementary combinatorial calculation)のところを。
内容:
- 具体例
- 生成元と関係
- 掛け算九九、いや掛け算五五
- テンパリー/リーブ電卓
- 2,3のコメント
●具体例
テンパリー/リーブ代数(Temperley-Lieb Algebra)は、係数環Rと、ループが生じたときの乗数τ(τ∈R)、それと点(釘)の数nで決まります。アブラムスキーのテキストでは、nを次元(dimension)と呼んでますが、誤解のもとのような気がするので、n次元テンパリー/リーブ代数じゃなくて、n点テンパリー/リーブ代数と呼ぶことにします。一番単純でしかし自明ではない例は n = 3 です。以下、n = 3、つまり3点テンパリー/リーブ代数だけ扱います。
ジョーンズ多項式を扱うには、係数環Rを1変数のローラン多項式環にとりますが、とりあえず整数係数でもいいでしょ(簡単だから)。τを1にするのが一番簡単だけど、ちょっとつまんない気もするのでτは2にします。
- 係数環=整数環Z
- ループの乗数τ=2
- 点の数=3
この具体例で、露骨に計算しましょう。
●生成元と関係
点の数が3だと、生成元の数は3 - 1 = 2個。U1, U2ですが、下付き添字が面倒なんでU, Wにします(Vを使わないのは、手書きのときUと紛らわしいから)。掛け算の計算法則は:
- UU = 2U
- WW = 2W
- UWU = U
- WUW = W
ここで、まったく形式的に(意味をはぎとって)考えて、文字'U'と'W'からなる列、例えば、UWWUWUUのようなものを考えます。上の計算法則を文字列の書き換え規則だとみなして、可能な限り短く書き換えることにします。ただし、2のような整数はどこにでも移動可能で並べると掛け算の意味になるとします。例えば:
- UWWUWUU ⇒ U(2W)UW(2U) ⇒ 4UWUWU ⇒ 4UWU ⇒ 4U
それ以上短くできない文字列を正規形と考えて、正規形を具体的に全部列挙します。なお、整数の部分は長さに勘定しませんから注意。
- 長さ0の正規形: 空列だけ
- 長さ1の正規形: U, W
- 長さ2の正規形: UW, WU
長さ3の文字列は、UUU, WUU, UWU, UUW, WWU, WUW, UWW, WWWの8個ありますが、どれも正規形ではなくて、長さ2以下に書き換え(還元)されます。
- UUU ⇒ (2U)U ⇒ 2(UU) ⇒ 2(2U) ⇒ 4U
- WUU ⇒ W(2U) ⇒ 2WU
- UWU ⇒ U
- UUW ⇒ (2U)W ⇒ 2UW
- WWU ⇒ (2W)U ⇒ 2WU
- WUW ⇒ W
- UWW ⇒ U(2W) ⇒ 2UW
- WWW ⇒ (2W)W ⇒ 2(WW) ⇒ 2(2W) ⇒ 4W
空列をIと書くことにすると、結局正規形は I, U, W, UW, WU の5つです。これで、Z加群としての3点テンパリー/リーブ代数の次元(階数)は5だとわかりました。3点テンパリー/リーブ代数の任意の元は、I, U, W, UW, WU の整係数1次結合で書けます。
●掛け算九九、いや掛け算五五
アブラムスキーは、UWを右波(right wave)、WUを左波(left wave)と呼んでいるので、UWをR、WUをLと略記します。I, U, W, R, L を絵に描いておけば:
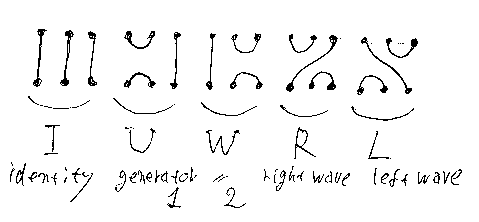
掛け算は、この図(カウフマン図)を縦に連結することなので、絵を描けば掛け算の表を作れます。掛け算九九じゃなくて五×五=二十五の表です。
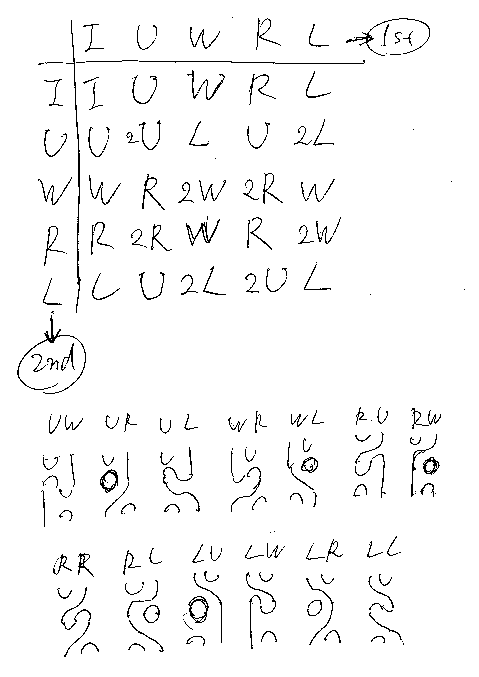
掛け算五五の表ができたので、表を見ながら掛け算をやってみました。
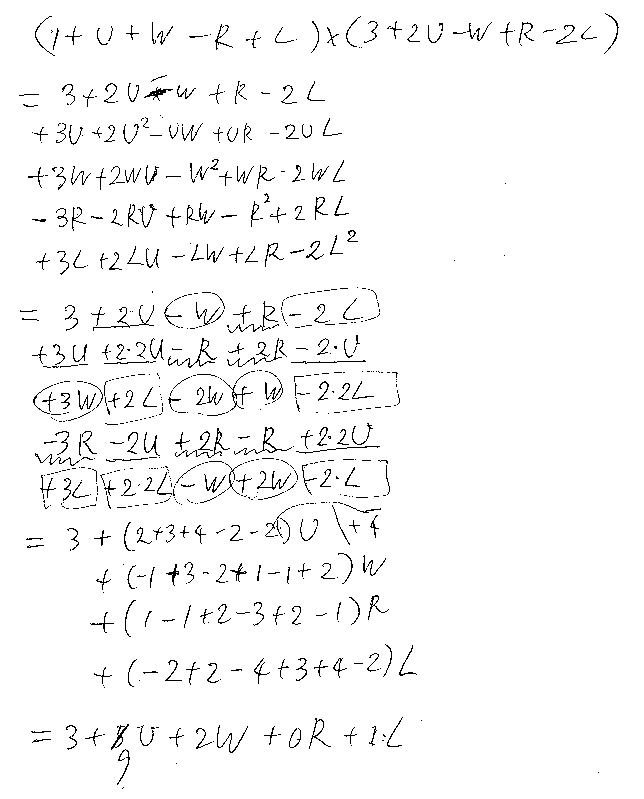
●テンパリー/リーブ電卓
手計算は大変なので、簡単なJavaScriptプログラムを作りました。a, b, c, d, eを5つの整数として、aI + bU + cW + dR + eL を長さ5の配列 [a, b, c, d, e] で表します。先の手計算は、[1, 1, 1, -1, 1] と [3, 2, -1, 1, -2] の掛け算ってことになります。multって関数でやってみます。
js> mult([1, 1, 1, -1, 1], [3, 2, -1, 1, -2])
3,9,2,0,1
js>
手計算と同じ答になりました*1。もっとも、手計算もプログラムも両方間違っている可能性はあるけど ^^; もし計算があっていれば、UIをもっとしゃれたものにすれば、テンパリー/リーブ電卓ができるでしょう。(って、いったい誰が使う?)
function makeMat(first, second) {
var r = new Array();
for (var i = 0; i < 5; i++) {
r[i] = new Array();
for (var j = 0; j < 5; j++) {
r[i][j] = first[i]*second[j];
}
}
return r;
}function mult(first, second) {
var mat = makeMat(first, second);
return [gatherI(mat),
gatherU(mat),
gatherW(mat),
gatherR(mat),
gatherL(mat)
];
}function gatherI(mat) {
return mat[0][0];
}function gatherU(mat) {
return (mat[0][1] +
mat[1][0] +
mat[1][1]*2 +
mat[1][4] +
mat[3][1] +
mat[3][4]*2
);
}function gatherW(mat) {
return (mat[0][2] +
mat[2][0] +
mat[2][2]*2 +
mat[2][3] +
mat[4][2] +
mat[4][3]*2
);
}function gatherR(mat) {
return (mat[0][3] +
mat[1][2] +
mat[1][3]*2 +
mat[3][0] +
mat[3][2]*2 +
mat[3][3]
);
}function gatherL(mat) {
return (mat[0][4] +
mat[2][1] +
mat[2][4]*2 +
mat[4][0] +
mat[4][1]*2 +
mat[4][4]
);
}
●2,3のコメント
hiroki_fさん曰く:
Temperley-Lieb algebraが行列で表現できない
いや、できるでしょ、がんばれば。僕はできないけど。
行列で表現するのはあきらめる。
あきらめないで、ジョニー。
それのファインマンンダイアグラムが∩∪と同一視できる
同一視できるとは言ってない。似てるでしょ?って程度。n点テンパリー/リーブ代数の元を、1次元空間上に配置されたn個の点の“運動”の記述とみなしましょう。縦方向が時間の流れね。そのとき、生成元Uiは、対消滅と対生成が閉じ込められた(単独では取り出せない)素過程だとみなせるでしょ。消滅と生成がいつも組み合わされているので、観測可能な粒子数は保存します。と、その程度のことです。
他のところで、なんか変なこと言ってしまったんですけど、また後で。
*1:実はウソです。手計算間違ってました。後で直した跡が残ってます。