フラクタルビスケット、ポアソンスパゲッティ
フラクタルの語源は
「ラテン語の動詞frangereは『壊れる』、すなわち不規則な断片ができるという意味」
なのだそうです。 >> http://www.biwa.ne.jp/~k-tochi/siryou/siryofra.html
それでは、実際にものを壊したときの破片は、どのような大きさに散らばるのでしょうか。
岩石に衝撃を与えて破壊するとその破片の大きさの分布はベキ分布になることが知られています。
ガラスのコップを硬い床に落として割った時にできる破片も同じです。
大きな破片はほんの数個で、中くらいの破片はかなりの数になり、小さな破片は無数にあります。
-- 経済物理学の発見(光文社新書)より.
試しにやってみようと思ったのですが、岩石を割るのはたいへんだし、ガラスのコップを割るのはもったいない。
簡単に割れるものを探してみたところ、戸棚の中にビスケットがありました。
小袋の中に入っている4枚のビスケットです。さっそく割ってみよう、アタァ〜!
割れた破片を大きさの順序に並べて整理します。
大きい方の破片は簡単なんですけど・・・
小さい方の破片は、いくらでも出てきます。最後の方はほとんど粉です。
大ざっぱではありますが、大きさ(長辺の長さ)でクラス分けして数を数えてみます。
もともとのビスケットの直径は6cm あります。
6〜3cm : 4個
3〜2cm : 6個
2〜1cm : 18個
1〜0.5cm: 19個
0.5〜0.25cm: 24個
0.25〜0.1cm: 178個
0.1cm〜 : 細かい粉がたくさん
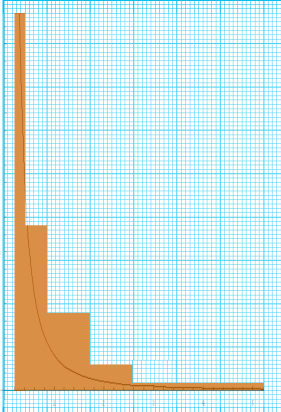
この集計結果をヒストグラムにすると、こんな風になりました。
ヒストグラムでは、面積が数に比例するように描かれています。
ヒストグラムの上に、ベキ分布の線が薄く重ねて描いてあります。
Y = 1 / x^2 の曲線を、ヒストグラムにフィットするように、目分量で拡縮して重ね合わせたものです。
なかなかよく一致していると思いませんか。
グラフには、最も小さい 0.25〜0.1cm の範囲が描かれていません。
グラフの枠から極端にはみ出してしまうからです。
実は、ベキ分布の曲線の方も、この範囲で大きくグラフの枠から外れます。
理論的には、グラフの曲線は0のところで無限大に発散します。
一方、ビスケットの破片の方も、細かい方には顕微鏡でなければ見えないような粉がいっぱい出てきます。
今回は1mm に満たない破片のカウントはあきらめました。
そんな細かい破片の様子を見ても、確かにビスケットの破片はベキ分布によく一致していると言えそうですね。
それでは、どんなものを壊しても、破片はフラクタルになる、つまり冪乗法則に従うのでしょうか。
前回の記事のコメントに、こんなことをいただきました。べき分布のメカニズム >> d:id:rikunora:20091130
「・・・ポアッソン分布になります。スパゲッティの麺を床に落として複数本に折れたときの長さの分布と同じです。」
スパゲッティを適当に折れば、冪乗法則ではなくて、ポアッソン分布というものになるらしい。
これもやってみました。まず普通のスパゲッティで試してみたのですが、
実はスパゲッティって思ったよりも丈夫で、都合良くポキポキ折れたりしないんです。
そこで、もっと細くて簡単に折れる“サラスパ”を使ってみました。
サラスパをお菓子の缶に入れて、その中に一緒に消しゴムと、マウスのボールを入れました。
フタをしてガラガラガラッと振ると、上手い具合にバラバラに折れてくれました。
折れたスパゲッティをお盆の上でソートします。
並べてみるとわかるのですが、見事なくらい綺麗な曲線を描きます。
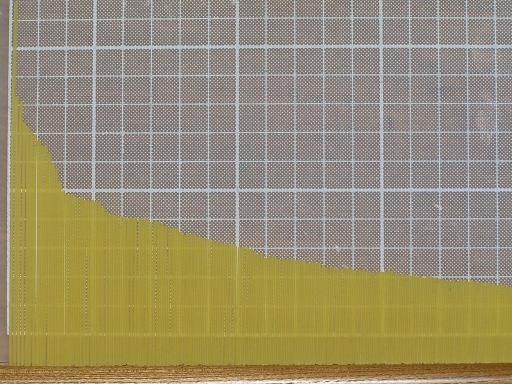


細かい粉の量は、明らかにビスケットよりも少ない。
並べ終えたところで、長さによってクラス分けした本数を数えてみました。
一番長いスパゲッティは 12.8cm でした
〜10cm : 1本
10〜 9cm : 2本
9〜 8cm : 4本
8〜 7cm : 5本
7〜 6cm : 4本
6〜 5cm : 23本
5〜 4cm : 27本
4〜 3cm : 50本
3〜2.5cm : 45本
2.5cm〜2cm: 39本
2〜1.5cm : 43本
1.5cm〜1cm: 39本
1cm〜0.5cm : 42本
0.5cm〜0.1cm: 26本
0.1cm〜 : 細かい粉
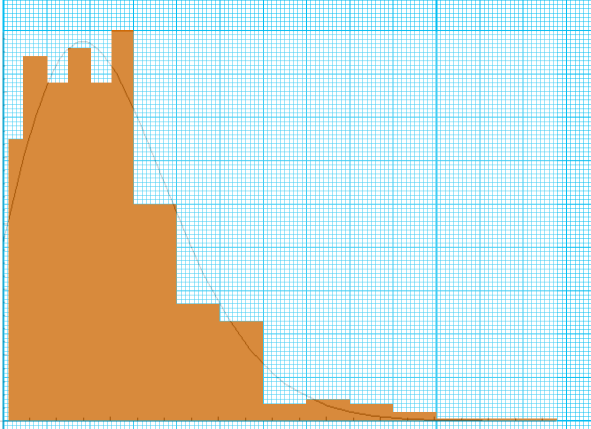
ヒストグラムにすると、こうなります。
グラフの形が、ビスケットとは大きく違っていますね。
ヒストグラムの上に、ポアソン分布の線が薄く重ねて描いてあります。
Y = Exp(-2)・2^x / Γ(x+1) の曲線を、ヒストグラムにフィットするように、目分量で拡縮して重ね合わせたものです。
確かに、実際のスパゲッティとよく一致していることがわかるでしょう。
正直、ここまでうまくグラフの形が出るとは思わなかった。理論恐るべし。
それ以前に、ビスケットとスパゲッティでこんな風に違っているなんて思わなかった。
両方とも、同じ小麦粉から作ってるのにね。
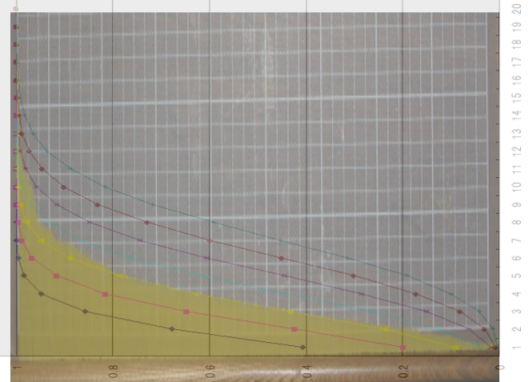
※2010/12/24追記: スパゲッティの曲線と、ポアソン分布の累積分布曲線を直接重ね合わせてみました。
Excelで、平均が2〜8の範囲でポアソン分布の累積分布曲線のグラフを作って、
目分量でスパゲッティの写真に重ねてみたものです。