2012-07-18

指数分布とガンマ分布

昨日からの続き
ガンマ分布の２つのパラメタを使うと、パラメタが１の指数分布のそれは $(\theta = 2, k = 1)$ と表される
こちらにあるように、互いに独立で同一な指数分布 $\frac{1}{\theta}e^{-\frac{x}{\theta}}$ に従う確率変数を $n$ 個合わせると $\frac{1}{(n-1)!\theta^n}x^{n-1}e^{-\frac{x}{\theta}}=\frac{x^{n-1}}{\Gamma(n)\theta^n}e^{-\frac{x}{\theta}}$ になるという
これは、ガンマ分布の２変数として $(\theta = \theta, k =1)$ が $n$ 個合わさって、 $(\theta = \theta, k = n)$ になった、という意味

2012-07-18

独立な確率変数の和の分散

分布

２つの独立な確率変数の和を考えるとき、期待値も和、分散も和(こちら)
２つの独立なガンマ分布の和の期待値と分散を考えよう
$\Gamma(\theta_1,k_1)$
$\Gamma(\theta_2,k-2)$
ガンマ分布の期待値と分散は $\theta k, \theta^2 k$ だから
２つのガンマ分布の和については
- $\theta' k' = \theta_1 k_1 + \theta_2 k_2$
- $(\theta')^2 k' = (\theta_1)^2 k_1 + (\theta_2)^2 k_2$ が成り立つから
- $\theta' = \frac{(\theta_1)^2 k_1 + (\theta_2)^2 k_2}{\theta_1 k_1 + \theta_2 k_2}$
- $k' = \frac{(\theta_1 k_1 + \theta_2 k_2)^2}{(\theta_1)^2 k_1 + (\theta_2)^2 k_2}$
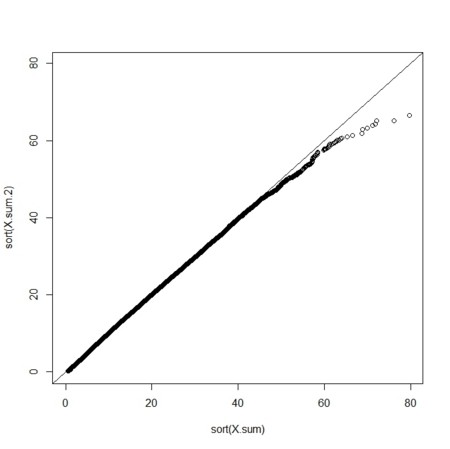
Rで確かめてみる

t1 <- runif(1) * 5
t2 <- runif(1) * 5
k1 <- runif(1) * 5
k2 <- runif(1) * 5
n.pt <- 100000
X1 <- rgamma(n.pt, shape = k1, scale = t1)
X2 <- rgamma(n.pt, shape = k2, scale = t2)
X.sum <- X1 + X2

t.sum <- (k1*t1^2+k2*t2^2)/(k1*t1+k2*t2)
k.sum <- (k1*t1+k2*t2)^2/(k1*t1^2+k2*t2^2)

X.sum.2 <- rgamma(n.pt,shape = k.sum, scale = t.sum)

xlim <- ylim <- range(c(X.sum,X.sum.2))
plot(sort(X.sum),sort(X.sum.2),xlim=xlim,ylim=ylim)
abline(0,1)