とある助教の2023年の年収
1年ぶりになってしまったブログ記事です。
2023年12月の給与明細
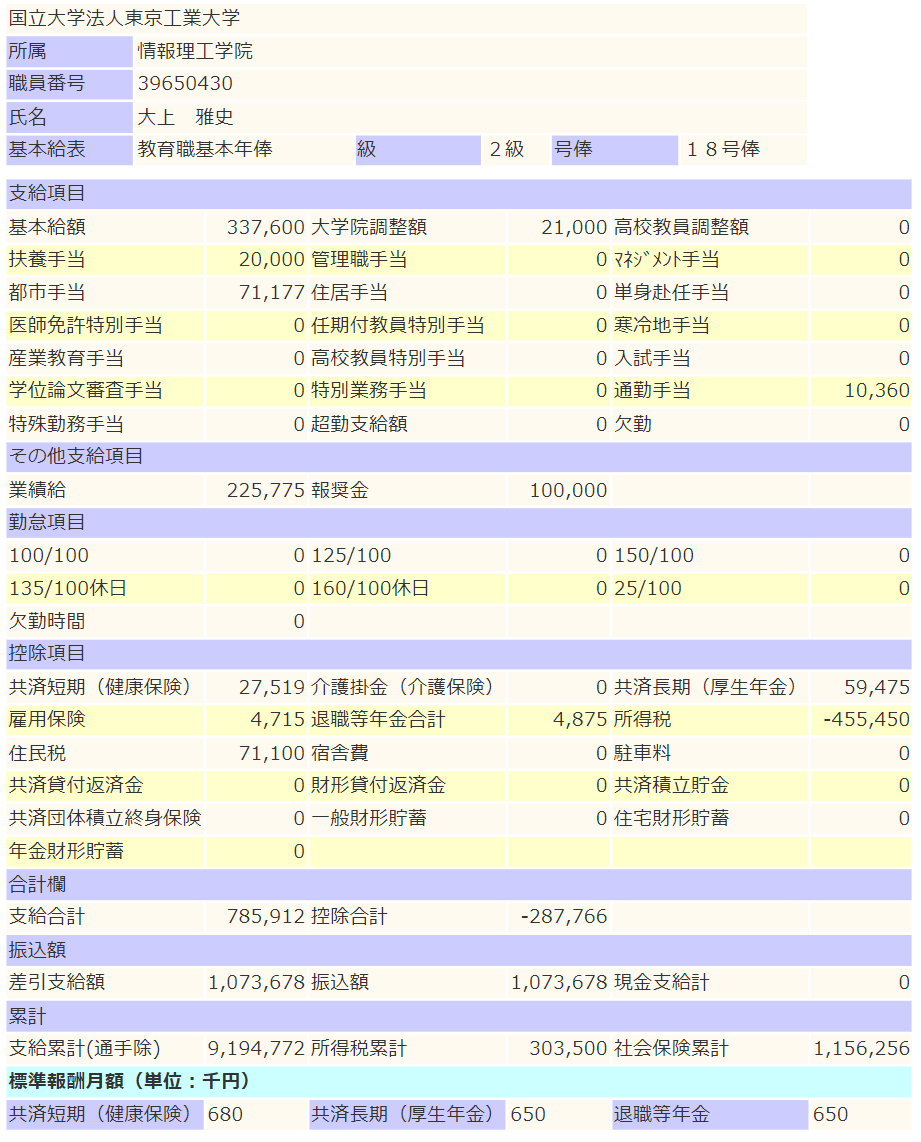
一部解説(12月分に記載のないものもあります)
- 裁量労働制という制度なので、定時や残業という概念はありません。
- いわゆる旧年俸制(退職金を先に払ってる年俸制)です。
- 基本給が年に12回払われます。
- ボーナスという概念が月々支払われる業績給に吸収されています。業績給は均されて定額が年に12回支払われます。
- 業績給に退職金を含んでいます。(通常の課税対象です)(退職時にもらえる退職金は0です)
- 任期付の教員ですが任期付教員特別手当が出ません。
- 子どもを2人扶養しているので扶養手当を頂いています。
- 都市手当というものが存在します。(基本給+大学院調整額+高校教員調整額+管理職手当+扶養手当)×18.8%で計算されます。
- 競争的研究資金からPI人件費を100万円出していますが、業績付加給付金という形で98万円支給されています。
- 東工大教育賞という賞をもらったときの副賞として報奨金を10万円もらえました。(もちろん課税対象です)
- いわゆる住宅ローン控除をほぼフルで活用しています。
- 一般生命保険料控除だけやってます。(iDeCoやってません)
前年度比で+16万円ですが、報奨金を引いたら賞味+6万円でした。
(とある助教の年収の記事は、今回で一旦終了としたいと思います。)
2024.1.1追記
2024年1月1日付で、東京工業大学 情報理工学院 助教から准教授に昇任しました。テニュアトラックの審査をクリアした形です。任期が無くなること以外には全く何も変わりませんが、引き続き皆様よろしくお願い致します。
— Ohue M/大上雅史 (@tonets) 2023年12月31日
とある助教の2022年の年収
35歳助教氏ワイ、年収900に副業と印税あるので待遇そのものは相変わらずあんまり困ってないが、任期付きなのと、退職手当は無い。 https://t.co/7x819rnBrc
— Ohue M/大上雅史 (@tonets) 2022年12月26日
こちらのエビデンスです。
(2021年のものはこちら)
tonets.hatenablog.com
2022年12月の給与明細

ペプチドとドッキングとAlphaFold
この記事は?→創薬 (dry) Advent Calendar 2022の5日目の記事です。 adventar.org
10年以上の年月と3,000億円超の費用を要する医薬品開発の期間とコストを削減するため、創薬の様々な場面でコンピュータによるインシリコ(in silico)解析が導入されている。特に通常の低分子化合物では、バーチャルスクリーニングによるヒット化合物の発見、標的分子と活性リガンドの構造情報を利用した分子設計によるリード化合物の最適化、物性や動態の予測・最適化に至るまで、様々な課題に対して計算論的手法が開発されてきた。かたやペプチドについては、低分子と比較するとやや「出遅れていた」状況であった。だが、近年の技術革新によりインフォマティクス技術を基盤としたペプチドの設計が実現しつつある。以下ではペプチド創薬に活用できる、ペプチドを対象としたインシリコ(in silico)解析技術を紹介する。
タンパク質-ペプチドドッキング
ドッキングシミュレーション(単にドッキングとも言う)は、標的となる分子と目的の分子の複合体構造を推定し、併せて標的親和性を計算によって評価するための方法論である。標的としてはタンパク質やRNA、目的の分子としては低分子や金属イオン、糖鎖などが該当し、たとえばタンパク質と低分子(タンパク質-リガンドドッキング)、タンパク質とタンパク質(タンパク質ドッキング)、タンパク質と金属イオン、タンパク質と糖鎖など、個々に手法が開発されている。このうち、タンパク質とペプチド(主に数残基~20残基程度のサイズ)を対象とした技術をタンパク質-ペプチドドッキングと呼ぶ。
タンパク質-ペプチドドッキングは、標的タンパク質に対するペプチド分子の結合様式(複合体構造)を推定し、その結合親和性をエネルギースコア等の値として評価するような手法を言う。いくつかのソフトウェアが提案されているが、なかでもAutoDock CrankPep*1が、数残基~20残基くらいまでのペプチドに対して精度良く複合体構造(図1)を推定可能であるとされている。

ドッキングソフトウェアから計算されるエネルギースコアの値の良し悪しで、ペプチドの標的タンパク質に対する結合能が評価できる。エネルギースコアは「タンパク質のどこにどんな形で結合しそうか」を評価するための計算値であるが、たとえば「目的のペプチドが、他のすでに知られている結合ペプチドや、ランダムな配列のペプチドと比較して、どのくらい結合能が高い(or低い)のか」を推定すること、すなわちバーチャルスクリーニングにも活用できる。
なお、ほとんどのドッキングソフトウェアでは直鎖かつ標準アミノ酸20種で構成されたペプチドしか扱うことができなかったが、最近ではD体アミノ酸や修飾のあるアミノ酸などの非標準アミノ酸を含んだペプチドや、ペプチド鎖の末端や途中で環状型になっているペプチド(環状ペプチド)についても入力として扱えるソフトウェアが増えてきた。AutoDock CrankPep(環状ペプチドに対する評価は文献*2を参照)やHADDOCK*3は、環状ペプチドに対するドッキングシミュレーションを実行可能なソフトウェアとしても使われている。
ところで、タンパク質立体構造予測の分野ではAlphaFold2による予測精度の革新があったことは記憶に新しい。実は現在のAlphaFold2は、タンパク質複合体(ホモ/ヘテロオリゴマー)の構造予測が可能となっており、タンパク質ペプチド複合体構造の予測にも使えそう(図2)だということが複数のグループによって検証されてきた*4*5*6。

世界で初めてAlphaFold2によるペプチドドッキングを報告したツイート。残念ながら後の論文からはreferされず。(英語でtweetしておけばよかった)あ、AlphaFold2でペプチドドッキングできちゃった pic.twitter.com/BkNs6davJR
— Ohue M/大上雅史 (@tonets) 2021年7月20日
特にこれらの報告の中で、従来のドッキングと同様にペプチドのバーチャルスクリーニングができる可能性が示唆されている。ただし、AlphaFold2の制限として直鎖・標準アミノ酸のペプチドしか扱うことはできないことに注意が必要である。さらなる応用として、たとえば2つのペプチド配列を入力して、より結合が強い方がタンパク質に結合するような結果が得られるという、競合ドッキング法(competitive binding)と呼ばれる方法も提案されている*7(図3)。
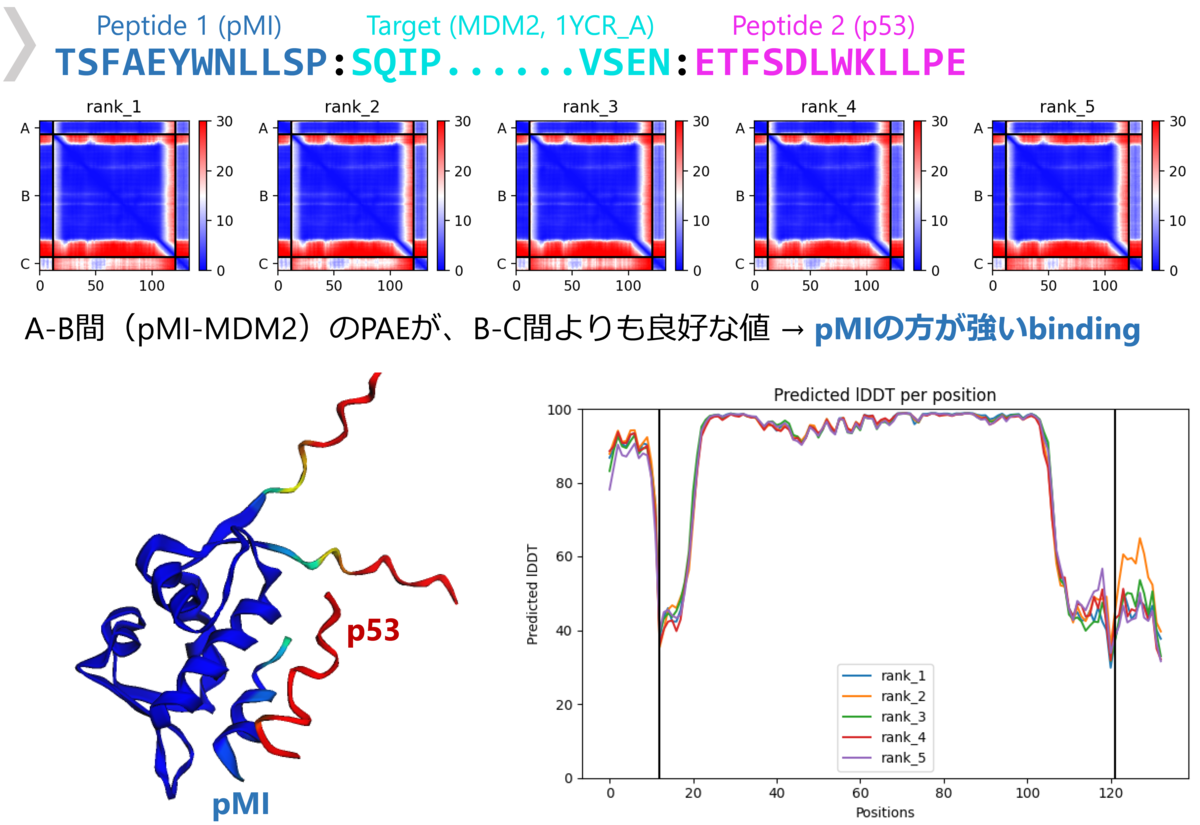
AlphaFold2によるペプチドデザイン
計算によって標的タンパク質に対するペプチドの結合能を評価することができるということは、手元にあるペプチド配列の比較だけでなく、あらゆるペプチド配列をソフトウェアに入力していくことで、標的タンパク質に対して結合能が高いペプチド配列が見つけられるということになる。ただしこのような発想で実際に網羅的にペプチド配列のスクリーニングを行う場合には、ペプチド残基長nに対して20ⁿ回の計算をする必要がある。10残基のペプチドだけを考えたとしても20¹⁰ ≒ 10兆通りのペプチド配列の評価が必要になり、これは非現実的である。対して、ランダムな配列からスタートし、予測の結果と欲しい構造との差を勾配としてフィードバックにして、フィードバックの結果から次の配列を選んでいくという方法(Hallucination法)*8が提案されており、予測値が良くなる方向にバイアスをかけて配列を選択することで、全通りの計算を避けて妥当なペプチド配列を生成することが可能になっている。
このアイデアに基づいて、Hallucination論文やRoseTTAFoldの著者でもあるSergey Ovchinnikovらによって実装されたAfDesignのbinder hallucination法で、実際にペプチド配列が生成できるようになっている。AlphaFold2の出力するペプチド複合体予測の評価値(pLDDTやPAEなど)を良くする方向にペプチド配列をサンプリングしていくことで、AlphaFold2的に良いと考えるペプチドを現実的な計算時間で生成するという仕組みである。実際にAfDesignを実行すると、実際に図4のようにペプチド配列が決定されていく様子を動画で出力することができる。

Adding support for binder hallucination if anyone wants to try! (Code is very experimental, not intended for practical use... only use for art/science) 😀https://t.co/OOPp8kSu2Z pic.twitter.com/WUu9LGKIwp
— Sergey Ovchinnikov @ NeurIPS 🇺🇦 (@sokrypton) 2022年2月3日
AlphaFold2による水溶性ペプチドデザイン
ところが、AfDesignによって生成された配列を確認すると、難水溶性のペプチドが多くを占めていた。タンパク質間相互作用の相互作用面は一般に疎水領域であり、AlphaFold2 (AlphaFold-Multimer) も相互作用面に共起しやすい残基の関係を学習していると考えられることから、タンパク質の表面に結合するペプチド配列をAlphaFold2によって設計しようとすると疎水領域を構成するように、すなわち疎水性残基を多用したペプチド配列が選ばれやすくなっているのだと解釈できる。だが、後の生化学実験などを考える上ではペプチドの水溶性は重要である。
我々はこの問題を解決するために、AlphaFold2の評価値に加えてhydropathy indexなどのアミノ酸に関する物性評価指標を導入し、「疎水性アミノ酸はあまり使わないように」といった形で残基の使用頻度を制御することで、適切なペプチド配列を生成する手法「Solubility-AfDesign」を提案した*9。Solubility-AfDesignによって、実際に標的結合能を維持したまま水溶性を向上させるペプチド配列の予測に成功し(図5)、具体的な複合体構造モデルとともに提示することができるようになった。この論文は日本語で以下に解説があるので、興味を持った方は読んで頂ければ幸いである。 blacktanktop.hatenablog.com
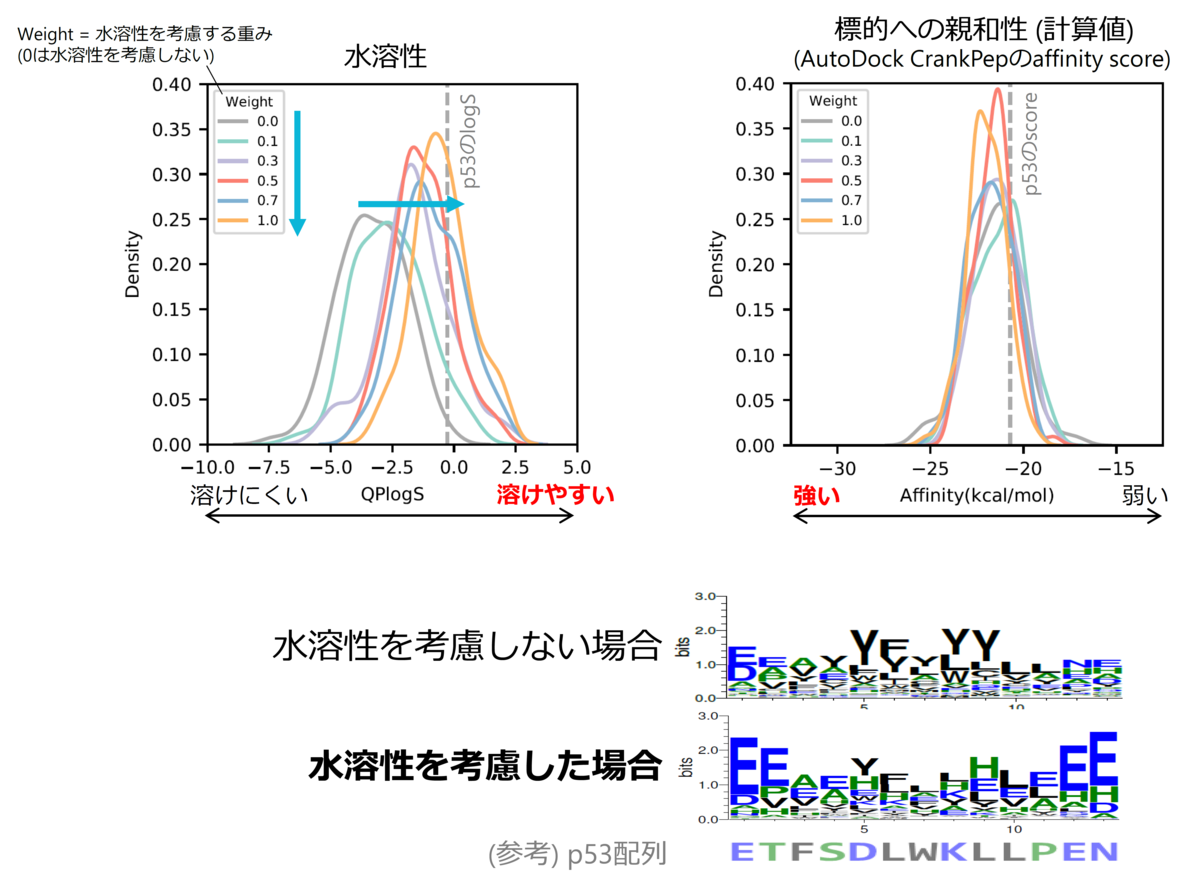
まとめ
本稿ではペプチドに関するin silico技術を紹介したが、ペプチドの計算技術・設計技術はまだまだ発展を続けている段階である。タンパク質構造、低分子、ペプチドと、それぞれでAIやシミュレーション技術が展開されてはいるが、まだまだin silicoが追いついていない領域でもあるかと思う。AlphaFold2やChromaのように突然すごいAI技術が降ってくるかもしれない。どれがイケててどれは微妙なのか、目利きも重要になるかと思う。今後の発展に目が離せない。
Today we introduced Chroma, a generative model that creates new proteins & protein complexes given geometric & functional constraints. It learns to transform unstructured, random 3D shapes into #protein molecules, which can have tens of thousands of atoms. https://t.co/cORRnRKnfB pic.twitter.com/2OUk9AOQuj
— Generate Biomedicines (@generate_biomed) 2022年12月1日
*1:Zhang Y, Sanner MF. AutoDock CrankPep: combining folding and docking to predict protein-peptide complexes. Bioinformatics. 2019;35(24):5121-5127. doi: 10.1093/bioinformatics/btz459.
*2:Zhang Y, Sanner MF. Docking Flexible Cyclic Peptides with AutoDock CrankPep. J Chem Theory Comput. 2019;15(10):5161-5168.
*3:Charitou V, van Keulen SC, Bonvin AMJJ. Cyclization and Docking Protocol for Cyclic Peptide-Protein Modeling Using HADDOCK2.4. J Chem Theory Comput. 2022; 18(6):4027-4040.
*4:Ko J, Lee J. Can AlphaFold2 Predict Protein-Peptide Complex Structures Accurately? bioRxiv 2021.07.27.453972, 2021.
*5:Tsaban T, Varga JK, Avraham O, Ben-Aharon Z, Khramushin A, Schueler-Furman O. Harnessing protein folding neural networks for peptide-protein docking. Nat Commun. 13(1):176, 2022.
*6:Johansson-Åkhe I, Wallner B. Improving peptide-protein docking with AlphaFold-Multimer using forced sampling. Front Bioinform, 2, 959160, 2022.
*7:Chang L, Perez A. AlphaFold encodes the principles to identify high affinity peptide binders, bioRxiv 2022.03.18.484931, 2022.
*8:Anishchenko I, Pellock SJ, Chidyausiku TM, Ramelot TA, Ovchinnikov S, Hao J, Bafna K, Norn C, Kang A, Bera AK, DiMaio F, Carter L, Chow CM, Montelione GT, Baker D. De novo protein design by deep network hallucination. Nature. 2021; 600(7889):547-552.
*9:Kosugi T, Ohue M. Solubility-aware protein binding peptide design using AlphaFold. Biomedicines, 10(7): 1626, 2022.
タンパク質間相互作用 (PPI) を標的とする化合物の設計
この記事は?→創薬 (dry) Advent Calendar 2022の4日目の記事です。 adventar.org
タンパク質間相互作用 (protein-protein interaction, PPI) が創薬標的として注目されるようになって久しい。一般に難しい標的とされているPPIであるが、近年は様々な計算技術とともにPPI標的化合物をうまく設計するための方法が発展してきている。この記事では、最近のPPI標的化合物設計におけるin silico手法を紹介したいと思う。
タンパク質間相互作用(Protein-Protein Interaction)を狙う低分子化合物
タンパク質間相互作用 (protein-protein interaction, PPI) はあらゆる生命現象に介在しており、創薬標的として高い注目を集めている。ヒトにおけるPPIは現時点で883,507件報告*1されており、今なお新たなPPIの発見が報告されている。実際にはこれらのPPIが全て潜在的な創薬標的となるわけではなく、当然ながら様々な理由により創薬標的として適さない(‘undruggable’な)PPIも多いため、実際に創薬標的とされているPPIの種類はわずかである。しかしながら、例えば複合体の立体構造が解かれてラショナルドラッグデザインが可能となっていく、低分子では阻害が難しかったPPIでも近年の新規医薬モダリティの発展によって阻害できるようになっていく、といった、近年および今後の状況の変化により潜在的なdruggable PPIはますます増えていくことが想定され、多様なメカニズムを持つPPIは今後ますます創薬研究に影響を及ぼすことと思われる*2。
従来の分子標的薬設計においては、タンパク質構造上の特定の結合サイト(例:基質結合ポケットなど)に対して化合物構造を設計するが、PPIを標的とする場合はより広い表面領域(相互作用インターフェース)を狙う必要がある。図1にPPIの例としてInterleukin-2とInterleukin-2受容体αの複合体構造を示す。

タンパク質間相互作用を標的とする化合物の設計指標
経口医薬品に関する設計指標 – RO5 と QED
LipinskiのRule-of-Five (RO5)*4は、経口医薬品が満たすべき性質の経験則としてよく知られている。RO5は以下の4つの記述子によるルールで構成されている。
いずれのルールも数字の5または5の倍数にちなむことから “Rule-of-Five” と名付けられている。このルールを2つ以上満たさないような化合物は吸収が悪く、最終的に医薬品になりづらいとされている。実用上は、LogP値は実験値ではなく計算による推定値を用いることがほとんどであり、CLogPやMolLogPがよく用いられる。
RO5は選ばれている分子記述子の計算が容易であり、記述子の種類も様々な物性との相関がよく知られているものであるため、創薬化学者にとっても理解しやすく、受け入れられやすい指標である。一方で、ルールに合うか合わないかという2値での分類をしているため、たとえば分子量501の分子と分子量1000の分子は同様に除外されてしまうという問題がある。実際には分子量501で若干オーバーしていたとしても全く医薬品として望ましくないというわけではないため、適合度合いをより定量的に評価することが重要である。このような医薬品らしさを定量評価する指標として、Bickertonらが2012年に提唱したQED*5がある。QEDでは771個のFDA承認薬(経口医薬品)から次の8種類の記述子の分布を求め、分布の頂点の値を取るような記述子の値を持っている分子は「薬らしい」と定義して0から1の値として定量化をしたものである。
- 分子量 (MW)
- オクタノール/水分配係数(脂溶性) (LogP)
- 水素結合ドナーの数 (HBD)
- 水素結合アクセプターの数 (HBA)
- 極性表面積 (PSA)
- 回転可能結合数 (ROTB)
- 芳香環の数 (AROM)
- 忌避構造の数 (ALERTS)
QEDに使われている記述子を見るとわかる通り、QEDで用いる記述子はRO5と共通する。これらの記述子も簡単に計算できるため、QEDは分子設計の上でよく用いられている指標となっている。たとえば新型コロナウイルス感染症治療薬として使われている合剤パキロビッド®パックに含まれるプロテアーゼ阻害剤ニルマトレルビル (Nirmatrelvir) について、各記述子およびRO5とQEDを計算したものが図2である。QED = 0.504という値はRO5を全て満たしている医薬品のQED値の分布から見るとやや低いものの、分布から外れた値というわけではない(詳細はQED論文のFigure 2(c)を参照)。
なお、それぞれの記述子の計算にはPythonライブラリであるRDKit version 2022.9.1を用い、以下のコードで計算した。特にLogPは推定値であるMolLogP、PSAは推定値であるトポロジカルPSA (TPSA) で代用した。
from rdkit import Chem m = Chem.MolFromSmiles(r'CCOC(=O)C1=C(N(C2=CC(=C(C(=C21)CN(C)C)O)Br)C)CSC3=CC=CC=C3') Chem.Descriptors.MolWt(m) # MW Chem.Descriptors.MolLogP(m) # LogP Chem.Descriptors.NumHAcceptors(m) # HBA Chem.Descriptors.NumHDonors(m) # HBD Chem.Descriptors.TPSA(m) # PSA Chem.Descriptors.NumRotatableBonds(m) # RotB Chem.Descriptors.NumAromaticRings(m) # AROM Chem.QED.properties(m).ALERTS # ALERTS # Chem.QED.properties(m) # これで全部出せる。ただしHBA/HBDの値はNumHAcceptors/NumHDonorsの値と異なる場合がある。(!?)
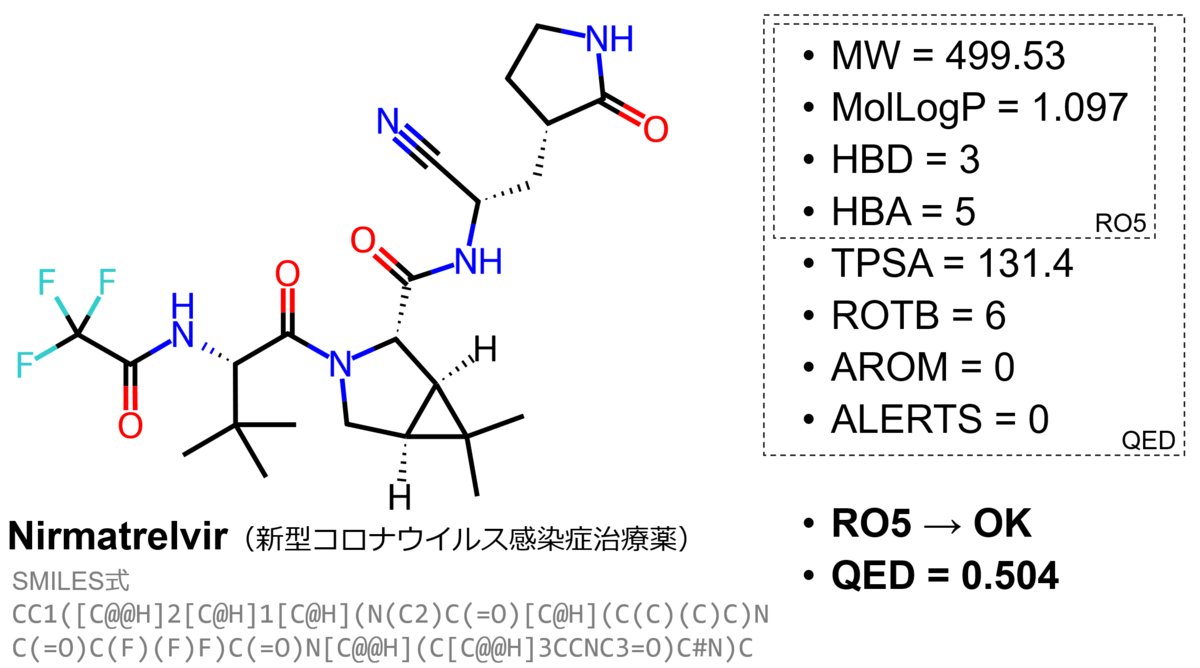
PPI標的化合物に関する設計指標 – RO4とQEPPI
RO5およびQEDは、経口医薬品の持つ統計分布や経験則を用いた指標であった。一方で、PPI標的化合物には通常の経口医薬品と比べても「分子量が大きめ」といった異なる特徴が求められる。実際に、MorelliらはPPI阻害剤39個のデータからPPI阻害剤が持つ記述子の経験則をRule-of-Four (RO4) という形で以下のようにまとめた*6。
いずれのルールも4にちなんでいることから “Rule-of-Four” と呼ばれている。RO4を満たすような化合物はPPI阻害剤になりやすい性質を有していると考えられる*7。
一方で、RO5とQEDの関係と同様に、定量的に判断できる指標は重要である。我々はQEDの考え方を参考にして、記述子の統計値をもとに「PPI標的化合物らしさ」を定量化できる指標としてQEPPI (https://github.com/ohuelab/QEPPI) を開発した*8。QEPPIでは、関数モデリングに先立ち、Morelliらが用いていたデータよりもより広範なデータを収集するため、論文等からPPI標的化合物を登録しているiPPI-DBを用い、ここから冗長性を省いた1,007化合物を選択した。これらのデータについてQED記述子のうちALERTSを除く7つの記述子の分布*9を求め、QEDと同様に関数モデリングを行って0から1の値としてPPI標的化合物らしさを定量化した。図3にiPPI-DB化合物に対するそれぞれの記述子のヒストグラムを描画し、分布関数を重ねたものを示す。QEDと比較して分布の山がいずれの記述子でも値が大きい方にずれていることがわかるかと思う。
QEPPIの具体的な例として、たとえばコロナウイルスのスパイクタンパク質とヒト細胞表面のACE2タンパク質との相互作用を阻害することが知られている抗ウイルス薬ウミフェノビル (Umifenovir) は、QED = 0.376と低めのQED値を示す一方で、QEPPI = 0.869と高いQEPPI値を示す(図4)。また、実際に開発されている臨床試験段階のPPI標的化合物についてQEPPI値を計算したところ、比較的高い値を示すこともわかった(図5)。
なお、それぞれの記述子の計算にはRDKit version 2022.9.1を用い、QEPPIは以下のPythonコードを用いて計算した。
from rdkit import Chem import QEPPI as ppi m = Chem.MolFromSmiles(r'CCOC(=O)C1=C(N(C2=CC(=C(C(=C21)CN(C)C)O)Br)C)CSC3=CC=CC=C3') q = ppi.QEPPI_Calculator() q.read() q.qeppi(m) # QEPPI #Chem.rdMolDescriptors.CalcNumRings(m) # * RING の計算は CalcNumRings()



タンパク質間相互作用向け化合物ライブラリー
PPIライブラリー
PPI標的薬の設計には、標準的な化合物ライブラリーではなく、PPI標的薬になりそうな化合物を集めたフォーカストライブラリーであるPPIライブラリーを用いる方が、ヒット化合物を得られる可能性が高くなると考えられる。単純に化合物ライブラリーからRO4を満たす化合物を選んで使うだけでも簡易的なPPIライブラリーとして活用できるが、特にタンパク質の相互作用面の特徴などから提案されたPPIライブラリーが、化合物サプライヤーから提供されている。以下に代表的なPPIライブラリーを4つ紹介する。
Enamine社が提供するPPIライブラリー (https://enamine.net/compound-libraries/targeted-libraries/ppi-library) はその代表例である。Enamine社のPPIライブラリーは、複数のタンパク質複合体構造を解析し、PPIに特徴的な二次構造やモチーフに特化して設計された化合物を集めたものであり、さらに忌避構造を含まないようにフィルタリングされ、実際に合成サンプルとして得られている化合物を約4万件収載している。
ChemDiv社が提供するPPIライブラリー (https://www.chemdiv.com/catalog/focused-and-targeted-libraries/protein-protein-interaction-library/) は、ペプチドミメティクスによる化合物や大環状型化合物、スピロ化合物などの特殊な母核構造も含むライブラリーであり、約21万件の化合物からなる。
UkrOrgSyntez社が提供するPPIライブラリー (https://uorsy.com/fragments-and-targeted-libraries/uorsy-ppi-modulators/) では、RO4を満たす化合物であり、PPI相互作用面におけるホットスポット残基であるTyr/Trp/Arg残基との相互作用が期待できる官能基を含む母核が含まれた、約6,500件の化合物からなる。
Life Chemicals社は、複数の方法で構築した多様なPPIライブラリーを提供する (https://lifechemicals.com/screening-libraries/targeted-and-focused-screening-libraries/ppi-libraries/)。実際にいくつかのPPIの相互作用面に対してドッキングシミュレーションを行うことによって構築したライブラリーや、RO4によるフィルタリングを行ったもの、公開されているPPI阻害アッセイで阻害能が確認された化合物と類似する化合物を集めたもの、独自に構築した機械学習による分類器で弁別したPPI標的化合物を集めたものなどが含まれている。
以上は化合物サプライヤーが提供するものであるが、公共データベースと論文情報から収集された既知のPPI阻害剤を含むPPIライブラリーとして、慶應義塾大学とペプチドリーム株式会社が共同で開発しているDLiP (https://skb-insilico.com/dlip) がある。DLiPでは、約15,000件のPPI阻害が期待できる化合物と、約26,000件の既知PPI阻害化合物の情報が収載されており、ウェブインターフェース上で検索や詳細閲覧が可能となっている。
PPIバーチャルライブラリー
低分子化合物の既存のライブラリーでも1億件以上の化合物が収載されている(例:ZINC15 in-stock library)が、化合物空間の多様性を考えれば化合物は無数に存在する*11。もちろんそのような化合物の中には合成が困難であったり創薬に適さない化合物も多々含まれるが、検討に値する化合物も大量に存在すると考えられる。そのような、これまでに合成されていないような化合物を計算によって「バーチャルに」生成することをde novo分子設計と呼び、機械学習の発展によって様々なde novo分子設計法が提案され、バーチャル化合物が生成されてきた。
de novo分子設計法の1つであるREINVENT*12は、リカレントニューラルネットワーク (RNN) に基づくSMILES文字列の生成モデルである。事前にChEMBLデータベースの化合物で学習したSMILES生成のための事前モデルから、あらかじめ決められた評価値が良くなる方向に学習を進める強化学習ステップによって、より良い評価値を持つ仮想的な化合物を生成するしくみとなっている。図6に我々がREINVENTを使ってQED、RO4(1ルールを満たすごとに+0.25として設計)、QEPPIの各値を評価値として与えて強化学習を行い、分子生成を行った結果を示す。QEDを良くするように設計されたバーチャル化合物は、当然ながら比較的分子量が小さく、LogPも低い傾向にある。一方でRO4を満たすように設計されたバーチャル化合物は、RO4が下限のみを定めるルールであることから分子量およびLogPが際限なく大きくなってしまうという問題がある。QEPPIでは分布から望ましい記述子の値を取るように設計されるため、QEDよりもやや分子量・LogPが大きい分子が生成されるが、たとえば分子量が1000を超えるような分子は生成されないことがわかる。我々はこのQEPPIに基づいてREINVENTで生成した化合物群を集めて、PPIバーチャルライブラリーとして公開する予定である。

まとめ
この記事では、タンパク質間相互作用を標的とする低分子設計を目指したいくつかの計算手法について紹介した。低分子化合物の創薬に役立つdry手法は、AI技術の発展とともに様々な面で発展し続けており、この記事で紹介した技術はほんの一端でしかない。タンパク質間相互作用はもはや狙えない標的ではないはずなので、これからも多くの薬が誕生することを願ってやまない。
謝辞
本記事の内容について、叢雲くすり氏 (twitter id @souyakuchan) より助言を頂きました。ここに感謝致します。
*1:BioGRIDデータベースから、生物種: Homo sapiens、Experiment type: PHYSICAL、Non-Redundant Interactions(異なる実験手法に基づく同一PPIの確認を単一カウントとする)によって検索した件数。(BioGRID version 4.4.215, 2022年11月現在)
*2:Scott DE, Bayly AR, Abell C, Skidmore J. Small molecules, big targets: drug discovery faces the protein-protein interaction challenge. Nat Rev Drug Discov, 15(8), 533-550, 2016.
*3:Thanos CD, DeLano WL, Wells JA. Hot-spot mimicry of a cytokine receptor by a small molecule. Proc Natl Acad Sci U S A, 103(42), 15422-15427, 2006.
*4:Lipinski CA. Lombardo F, Dominy BW, Feeney PJ. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv Drug Delivery Rev, 23(1-3), 3-25, 1997.
*5:Bickerton GR, Paolini GV, Besnard J, Muresan S, Hopkins AL. Quantifying the chemical beauty of drugs. Nat Chem, 4(2), 90–98, 2012.
*6:Morelli X, Bourgeas R, Roche P. Chemical and structural lessons from recent successes in protein-protein interaction inhibition (2P2I). Curr Opin Chem Biol, 15, 475–481, 2011. なおこの論文で言及されている2P2Iデータベースは、今はアクセスができない(汗)。
*7:Morelliらが解析したPPI阻害剤は論文等で報告されたものに基づいており、一部を除いて臨床試験段階には到達していない。その意味で、RO4が医薬品としての適正を担保するわけではないため注意が必要である(たとえば生物学的利用能は低くなることが予想される)。
*8:Kosugi T, Ohue M. Quantitative Estimate Index for Early-Stage Screening of Compounds Targeting Protein-Protein Interactions. Int J Mol Sci, 22(20), 10925, 2021.
*9:一般に分子量が大きくなるとその分忌避構造としてカウントされる部分構造を保有する確率も上がるため、ALERTSは分子量と相関し、PPI標的化合物では平均的に高い値になると考えられる。しかし、iPPI-DBに収録されている化合物のALERTSの平均値は、経口医薬品のALERTSの平均値よりも低くなるという、直感に反する結果が得られた。このことから、(初期の段階ではALERTSが低い化合物が優先的にアッセイにかけられている可能性など、)iPPI-DBのデータにはALERTSに関する選択的バイアスがあると考え、QEPPIのモデリングからALERTSを除外した。
*10:Truong, J.; George, A.; Holien, J.K. Analysis of physicochemical properties of protein-protein interaction modulators suggests stronger alignment with the “Rule-of-Five”. RSC Med Chem, 12, 1731-1749, 2021.
*11:RO5を満たす薬理活性化合物だけを考えた場合でも、潜在的に個超の化合物が存在すると推定されている。
*12:Blaschke T, Arús-Pous J, Chen H, Margreitter C, Tyrchan C, Engkvist O, Papadopoulos K, Patronov A. REINVENT 2.0: An AI Tool for De Novo Drug Design. J Chem Inf Model, 60(12), 5918-5922, 2020.
IQ1の助教の2021年
これの"年収部分"のエビデンスです。34歳助教氏ワイ、年収800に副業と印税あるので待遇そのものはあんまり困ってないんですよね。しいて言えば任期付きなのと退職手当が無い。
— 大上雅史|Ohue M (@tonets) 2022年2月20日
(2019年のものはこちら) tonets.hatenablog.com
2021年12月の給与明細

学振特別研究員と科研費の関係(学振PDと科研費「研究活動スタート支援」の関係)
学振特別研究員(DC1, DC2, PD, RPDなど)は、日本学術振興会 科研費(特別研究員奨励費)がもらえます。
加えて、学振PDは科研費(文部科学省/日本学術振興会 科学研究費助成事業)全般の応募資格を得ることができるため、その他の種目の科研費への応募が可能となっています。 *1
学振PDが研究代表者として申請できる科研費の種目は、
- 新学術領域研究(研究領域提案型)の公募研究
- 基盤研究(B)
- 基盤研究(C)
- 挑戦的研究(萌芽)
- 若手研究
の5種目です(令和2年度現在*2)。
ただし、科研費の応募資格は受入研究機関が付与するもので、学振PDになったからといって自動的にはついてきません。上記種目へ応募したい場合は、科研費の応募資格を取得する必要があります。
また、科研費の中には、新しく科研費の応募資格を得た新任の研究員や教員などが応募できる「研究活動スタート支援」という種目もあります。「研究活動スタート支援」は学振PDは応募ができません。11月締切の科研費応募以降に新たに研究者となった人(=応募資格を得た人)が応募できる5月締切の種目です。学振PDも新たに研究者となった人に違いないのですが、学振PDは「研究活動スタート支援」に応募することができないと決まっています。
このことがあり、科研費「研究活動スタート支援」と学振PDは関係がやや複雑です。
学振PDが科研費の応募資格を得るかどうかは本人の判断によります。つまり、学振PDの間に科研費の応募資格をあえて取得せずに、学振PD後で科研費の応募資格を得ることで研究活動スタート支援に応募できる可能性があります。シナリオとしては以下の2通りが考えられます。
- 学振PDの間に、科研費「若手研究」等に応募したり研究分担者として他の人の科研費等に参画しようと思って、科研費の応募資格を得る。その場合、学振PD後に助教などになっても研究活動スタート支援には応募できない。
- 学振PDの間に、科研費の応募資格を得ていなかった場合、その後の身分で11月上旬~5月上旬の期間で科研費の応募資格を新規に得れば、研究活動スタート支援に応募できる。
ちょっと罠っぽいですが、学振PDに内定したら考えておきましょう。
根拠資料
- 研究活動スタート支援 公募要領・計画調書 | 科学研究費助成事業|日本学術振興会
https://www.jsps.go.jp/j-grantsinaid/22_startup_support/download.html
- 対象者:文部科学省及び日本学術振興会が9月に公募を行った研究種目の応募締切日(令和2年は11月7日)の翌日以降に科学研究費助成事業の応募資格を得たため、当該研究種目に応募できなかった者
- 日本学術振興会特別研究員(SPD・PD・RPD・CPD)は「研究活動スタート支援」に応募することはできません。
- 日本学術振興会特別研究員又は外国人特別研究員である「科研費(特別研究員奨励費)」の研究代表者が、「研究活動スタート支援」の応募資格を有した場合(例えば、助教等に採用され、特別研究員又は外国人特別研究員の資格を喪失した場合)、本研究種目への応募は可能ですが、採択された場合には、交付内定通知受領後直ちに特別研究員奨励費の研究課題を廃止しなければなりません。
新米PIの1年をまとめた
註 まとまってない。
新米PIの2020年
2020年4月から、職位はそのままでラボを待つことになりました。いわゆるテニュアトラックという制度で、5年で審査を通ればテニュア化されるというものに乗っかっています。
2019年度
2019年度は私の任期の最終年度(ただし再任はあり)だったので、公募落ちたらそのまま助教やってようと思って准教授公募に4件応募しました。全部駄目でした。業績が足りません。
テニュアトラック化
弊大学の任期付き助教には再任期間を「テニュアトラック」にできる制度がありました。テニュアトラックというのは、がんばればテニュア=任期無しになるというものです。和訳すると「任期無しへの道」ですかね。
テニュアトラック化の審査を受けて通してもらったので、晴れて助教(テニュアトラック)になることになりました。うちの学部(学院)ではテニュアトラックの助教は准教授見習い扱いとしてラボを持つことが認められていたので、晴れてPIになることが決まりました。これが決まったのが2020年初めくらいのことです。
ラボ開きの前の準備
独立性を保つためという名目で、それまでのキャンパス(おおおおかやま)を離れ、すずかけ台キャンパスに着任することが確定してました。学院が持っている部屋の情報は簡単に調べられるので、おそらく自分に充てられるであろう部屋もおおよそ検討がつきました。その部屋に直接行ってみるとほんとに何もなく、床もwet実験用みたいな状態で、机も何もありませんでした。テニュアトラック化と言えど職位はそのままのただの任期延長で、さらに前例もあり、スタートアップ用の経費措置なんて無いことも予想が付いてました。
これを見越して、2019年の夏は財団にひたすらグラント応募をしてました。7件くらい。秋は科研費の調書を必死で書きました。什器や運搬にも使える「法人運営費(校費)」はほとんど手をつけず大事にとってありました。それでも、助教が持っている校費なんて吹けば飛ぶような額なので、2019年度で終了する学内事業や退官される先生ともやりとりをさせて頂きました(机や棚のお下がりが貰えるかもしれないので)。
とりあえず人間が過ごせる環境を作るために、家電と什器と床をなんとかしました。おおおおかやまにあるモノは赤帽さんに運んでもらいました(安い!)。机や椅子や棚は各所から譲っていただけて、出費がめちゃくちゃ抑えられました。カーペット敷くだけで数十万とかかかるんですね…
至る所で助教(PI)という話がレアケースで、たとえば学内運用のウェブサーバ1つ借りるだけでも「管理者は常勤の講師以上」みたいな制約に引っかかりました。早めに動かないと簡単に詰みます。PIは大変だ。
ウェブサイトを作り、ドメインも準備し、研究室にLANを配備し、電話回線を引き、什器と家電の手配を進め、合間に研究室紹介の素材を作ったり、もちろん2020年3月31日まではラボ付き助教なのでラボの研究その他も普通にしたり。何やってたっけと思い出せない程度に色々やりました。
ラボスタート
4月になり、ラボが始まりました。が、コロナでほとんどラボに行くことはありません。学生もB4が1人配属されましたが、完全リモート方針で進めています。
テニュアトラックの5年間の間に論文10報以上(内1stが5報以上)というのが条件の一つになっています。とにかく論文が出ないことには話にならないので、論文を書きます。
ぶっちゃけすずかけ台は遠いので(片道軽く1時間)、在宅ワークになって助かった面もあります。3月末に第二子も産まれてたので、在宅ワーク&学会出張無しという異例の2020年は、我が家には大変都合が良かったと思います。
10月ごろからは週2〜3くらいでラボに行って、止まっていた部屋の片付けやら工事手配を進めています。研究関連の物品の調達も進めていますが、応募していた財団助成金や科研費が採択されたのが本当にありがたく、これがないとマジで辛かったと思います。(過去の自分偉い)
2020年の総括
- 論文 7報(うち1st 3報)
- 総説 1報
- グラント 4件
- 家族++;
論文などは基本的に前所属の遺産の食いつぶしで得ている成果なので、自ラボの成果と呼べる論文を2021年に3報以上出すのが目標ですかね。2021年度は学生もさらに増える予定なので、もっと活動を広げていきたいと思っています。
(あとで追記するかも)