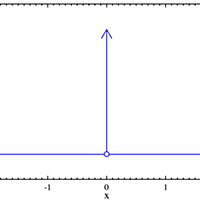
デルタ関数
(サイエンス)
【でるたかんすう】
ディラックにより導入された関数.
家電を例に取って説明すると、テレビのスイッチを入れた時にすぐに画面が安定して映る事はない。パチッと明るくなって、そして画面がじょじょに安定する。その現象を数学的に表すときに使う。
一瞬の衝撃などを表す、スパイク関数。全く滑らかではなく、特異的であるため、従来の数学では扱えなかったが、シュワルツなどにより理解が深まり、その後微分方程式を初めとして現代数学に欠かせない言葉の一つとなった。
線形システムの応答を知る上で理想的な入力関数でもある。
いわゆる普通の意味での関数ではなく,実際は「超関数」というクラスの元であることに注意。
構成
関数の極限操作から得られる
で
とした極限
数学的な定義
は
に対して
と定義される線形汎関数である。
リスト::数学関連