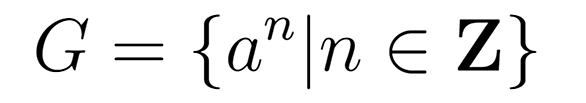準同型写像
(サイエンス)
【じゅんどうけいしゃぞう】
二つの群 G , G ' と、その間の写像 f : G → G ' について、f(gh) = f(g)f(h) が任意の g,h ∈ G について成り立つとき、f を G から G ' への群準同型写像、あるいは単に群準同型という。群の文脈であることが明らかならば、単に準同型写像、準同型などという。
また、G , G ' が共通の作用域 Λ を持つとき、任意の g ∈ G と任意の λ ∈ Λ に対して f(λ(g)) = λ(f(g)) が成り立つような準同型を Λ-準同型という。
一般には代数系の構造を保存して移す写像を準同型という 2つの代数系 ,
のすべての演算に対して次が成立つとき、
は代数系
から
への準同型写像であるという。
上のn-項演算
に対して対応する
上のn-項演算
が存在して、
が任意の元
に対して成り立つ。
リスト::数学関連