ここまでの一連のハイパーインフレーションモデルに関するエントリでは、基本的にローマーを参照し、貨幣需要関数としてケーガンの関数を用いてきた。一方、これらのエントリのきっかけとなった岩本康志氏のモデルでは、もっと簡単な
という貨幣需要関数を用いている。今日はこの関数について少し考察してみたい。
上式を時間で微分すると
という関係が導かれる。
一方、名目貨幣成長率gMと実質貨幣成長率の間には
の関係があるので、これに上式を代入すると
となる。これがπについての微分方程式であり、3/17エントリでケーガンの関数から導いたものより少し複雑な形になっている。
上式を変形すると
となるが、gM一定を仮定して、不定積分の公式
を用いると
が求まる(Bは定数)。この場合、πは有限時間[0, -(1/agM)ln(B) )で定義され、時間が経過するにつれ発散していく。
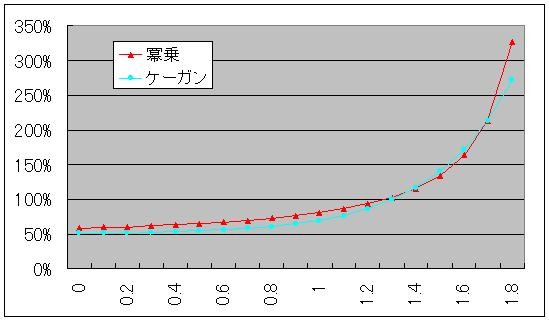
下図は、3/21エントリでシミュレートしたケーガンの貨幣需要関数をベースにしたπと、それとなるべく合わせるようにパラメータを調整した今回の冪乗の貨幣需要関数のπを並べて描画したものである。ここでgMは0.5固定であり、aは岩本氏と同様に2とした。Bは0.14と設定したので、時間の上限は-(1/(2*0.5))*ln(0.14)=1.97となる。
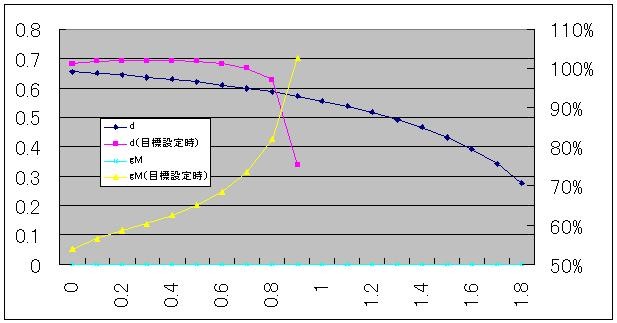
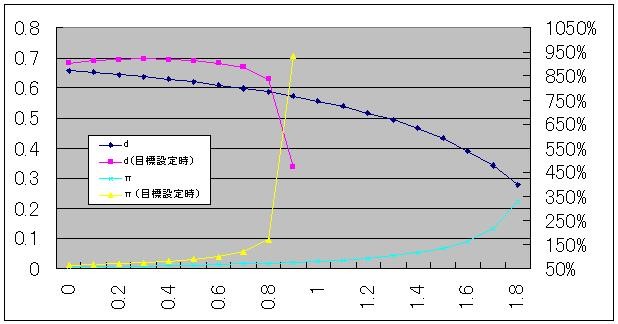
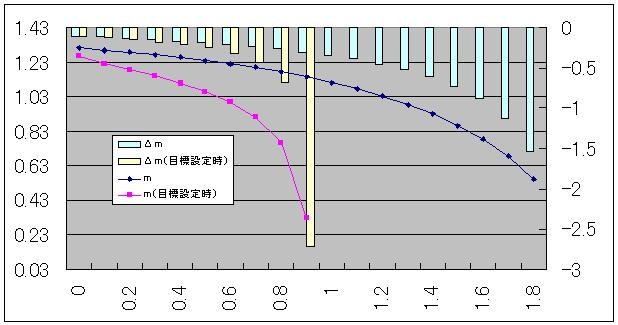
以降の図は、3/21エントリで実施したのと同じシミュレーションを、今回の関数について実施したものである。dの目標値は、前回同様、貨幣需要関数にπ=0.5を代入したものに0.5を掛け合わせて求めた(=0.707)。今回の貨幣需要関数には前回のCに相当する係数が無いため、mとdの縮尺が前回のおよそ10倍になっている。
今回の関数では、dに目標を設定すると、t=1に達したところで早くも発散して計算不能になってしまう。これは、今回の場合は時間の限界が有限で、gMを高めていくと、それが短縮されてしまうためである。そのため、ハイパーインフレーションがより劇的な形で現れた格好になっている。