数学・コンピュータ関連の姉妹ブログ『ryamadaのコンピュータ・数学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

周期性と巡回行列

巡回行列 フーリエ変換 固有値分解 周期性
  • 周期性というのは時間に関して、時刻間の差によって観察値の違い(ばらつき)が規定され、その時刻の差は周期のmoduloとして定められる者と言える
  • 時刻ごとの観察を変数として並べ、それらの関係を分散共分散行列として表すと、その行列は巡回行列になる
    • Rで作ればこんな感じ
      • まずは、どのセルにどんなのが入っているかに注意して作る
# 変数の数
n <- 6
L <- round(runif(n),2)
sigma <- matrix(0,n,n)
for(i in 1:n){
	tmp <- (1:n+i-2)%%n+1
	sigma[cbind(tmp,1:n)] <- L[i]
}
L
sigma

> L
[1] 0.10 0.56 0.30 0.68 0.71 0.01
> sigma
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.10 0.01 0.71 0.68 0.30 0.56
[2,] 0.56 0.10 0.01 0.71 0.68 0.30
[3,] 0.30 0.56 0.10 0.01 0.71 0.68
[4,] 0.68 0.30 0.56 0.10 0.01 0.71
[5,] 0.71 0.68 0.30 0.56 0.10 0.01
[6,] 0.01 0.71 0.68 0.30 0.56 0.10
    • 次に巡回行列をこんなルールで作る
      • C=c_o I + c_1 P + c_2 P^2 + ... + c_{n-1} P^{n-1}
        • ただしPは(i,i-1)と(1,n)に１が立ち、それ以外は0の巡回行列
P <- diag(rep(1,n))
P <- P[,c(2:n,1)]
P
sigma2 <- diag(L[1],n)
tmpP <- diag(rep(1,n))
for(i in 2:n){
	tmpP <- tmpP %*% P
	sigma2 <- sigma2 + L[i]*tmpP
}
sigma2
sigma

> P
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    0    0    0    0    0    1
[2,]    1    0    0    0    0    0
[3,]    0    1    0    0    0    0
[4,]    0    0    1    0    0    0
[5,]    0    0    0    1    0    0
[6,]    0    0    0    0    1    0
> sigma2
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.10 0.01 0.71 0.68 0.30 0.56
[2,] 0.56 0.10 0.01 0.71 0.68 0.30
[3,] 0.30 0.56 0.10 0.01 0.71 0.68
[4,] 0.68 0.30 0.56 0.10 0.01 0.71
[5,] 0.71 0.68 0.30 0.56 0.10 0.01
[6,] 0.01 0.71 0.68 0.30 0.56 0.10
> sigma
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.10 0.01 0.71 0.68 0.30 0.56
[2,] 0.56 0.10 0.01 0.71 0.68 0.30
[3,] 0.30 0.56 0.10 0.01 0.71 0.68
[4,] 0.68 0.30 0.56 0.10 0.01 0.71
[5,] 0.71 0.68 0.30 0.56 0.10 0.01
[6,] 0.01 0.71 0.68 0.30 0.56 0.10
  • ここで上でLとした、巡回行列のセルの値をc=(c_0,c_1,...,c_{n-1})=(L[1,L[n],L[n-1],...,L[2])]として
  • これの固有値分解をしたものは、w^n=1のn個の根w_i;i=0,1,...,n-1を使って\lambda_j = c_0 = c_{n-1}w_j + c_{n-2}w_j^2+...+c_1 w_j^{n-1}で得られるという
    • Rでやってみる
eigen.out <- eigen(sigma)
ws <- exp(2*pi*1i*(0:(n-1))/n)
lambdas <- rep(0,n)
for(i in 1:n){
	lambdas[i] <- sum(L[c(1,(n):2)] * ws[i]^(0:(n-1)))
}
eigen.out[[1]]
ord <- order(Mod(lambdas),decreasing=TRUE)
lambdas[ord]

> eigen.out[[1]]
[1]  2.36+0.0000000i -0.01+0.8313844i -0.01-0.8313844i -0.80+0.1212436i
[5] -0.80-0.1212436i -0.14+0.0000000i
> ord <- order(Mod(lambdas),decreasing=TRUE)
> lambdas[ord]
[1]  2.36+0.0000000i -0.01+0.8313844i -0.01-0.8313844i -0.80-0.1212436i
[5] -0.80+0.1212436i -0.14+0.0000000i
  • こうしてみてくると巡回行列は、ぐるり１順を表す行列Pのべきに係数重みをつけた行列であって、"unitary discrete Fourier transform matrix"というのを使うと、任意の巡回行列が、そのunitary discrete Fourier transform matrix (Un)とそのユニタリ行列とそれに挟まれた対角行列の積に分解できることがわかり(これは固有値分解)、その対角行列もfourier transform matrixと元の順が居行列の第１列(それに巡回行列の情報はすべて載っている)との積で簡単に得られる、という構造になっている
    • Rでやってみる
# 正方行列を作る。fourier transform matrixやその部品
U <- F <- matrix(0,n,n)
U.address <- which(U==0,arr.ind=TRUE)-1
# この部分の計算が、「２つの時刻j,jを用いたフーリエ的計算」になっている
f.jk <- exp(-2*U.address[,1]*U.address[,2]*pi*1i/n)
F <- matrix(f.jk,n,n)
U <- F/sqrt(n)
# 巡回行列sigmaの第１列だけ使っている
S <- F %*% matrix(sigma[,1],ncol=1)
# 固有値分解を再計算して、元の巡回行列と比較、計算機誤差以外は一致
t(Conj(U)) %*% diag(c(S)) %*% U
sigma

> sigma
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.10 0.01 0.71 0.68 0.30 0.56
[2,] 0.56 0.10 0.01 0.71 0.68 0.30
[3,] 0.30 0.56 0.10 0.01 0.71 0.68
[4,] 0.68 0.30 0.56 0.10 0.01 0.71
[5,] 0.71 0.68 0.30 0.56 0.10 0.01
[6,] 0.01 0.71 0.68 0.30 0.56 0.10
> t(Conj(U)) %*% diag(c(S)) %*% U
        [,1]    [,2]    [,3]    [,4]    [,5]    [,6]
[1,] 0.10-0i 0.01-0i 0.71+0i 0.68+0i 0.30-0i 0.56+0i
[2,] 0.56+0i 0.10-0i 0.01-0i 0.71+0i 0.68+0i 0.30-0i
[3,] 0.30+0i 0.56+0i 0.10-0i 0.01-0i 0.71+0i 0.68+0i
[4,] 0.68-0i 0.30-0i 0.56+0i 0.10-0i 0.01-0i 0.71+0i
[5,] 0.71+0i 0.68+0i 0.30+0i 0.56-0i 0.10-0i 0.01+0i
[6,] 0.01-0i 0.71+0i 0.68+0i 0.30+0i 0.56+0i 0.10-0i

すかすかなこと、と、神に託された不等式

調和解析 フーリエ変換 ウェーブレット変換 推定 James Stein推定 Sparcity Oracle inequalities 逆問題 時系列解析 Besov space ウェーブレット縮退
  • これの続き
  • こちらがPDF
  • まだうまく読めるかどうかわからないので、ひとまず登場する用語をメモ
  • 調和解析,フーリエ変換,ウェーブレット変換,推定,James Stein推定,Sparcity,Oracle inequalities,逆問題,時系列解析,Besov space,ウェーブレット縮退
  • Karhunen-Loeve decomposition

Wienerフィルタ、カーネル法、スムージング

Wienerフィルタ
  • 上記は、正規分布を仮定してそれにWienerフィルタをかませること。それはスペクトル分解して、その「主だったもの」を取り出すこと。そしてそれは正規分布の場合には全観測点をにらみあわせたときの最適推定になっていること。正規分布でないときには、最小二乗法で誤差の大小を評価する場合には、「線形推定の中では、最もよい」方法であることを説明するための道具立て
  • カーネル分布推定は、カーネル関数を使った畳みこみで、フーリエ変換の枠組みで表現することもできるから、同じこと。カーネル関数は形は決まるがその幅は可変なので、その幅として適当な値を探すことが推定作業
  • スムージング・スプライン法はフィッティングのよさと平滑のよさとを勘案するための重みづけを定めた最適化する。カーネル法も「(１変数)最適化」、スプライン法も「(１変数)最適化」
  • スプライン法は、等時間間隔の場合は離散フーリエ基底分解に相当し、非等時間間隔の場合のこのカウンターパートはDemmler-Reinsch systemというらしい

条件付期待値

条件付き期待値
  • 関連する事項として以下、確認
  • 条件付期待値(Wiki記事)
  • 以下の例でやってみよう
    • Xは平均0、分散d^2の正規分布に従っている。このXを観測誤差Z(ただし、平均0、分散s^2の正規分布に従う)を伴ってYと観察するとする
    • Yを観測した下でのXの期待値が\hat{X}|Y = \frac{d^2}{d^2+s^2}Yであるという
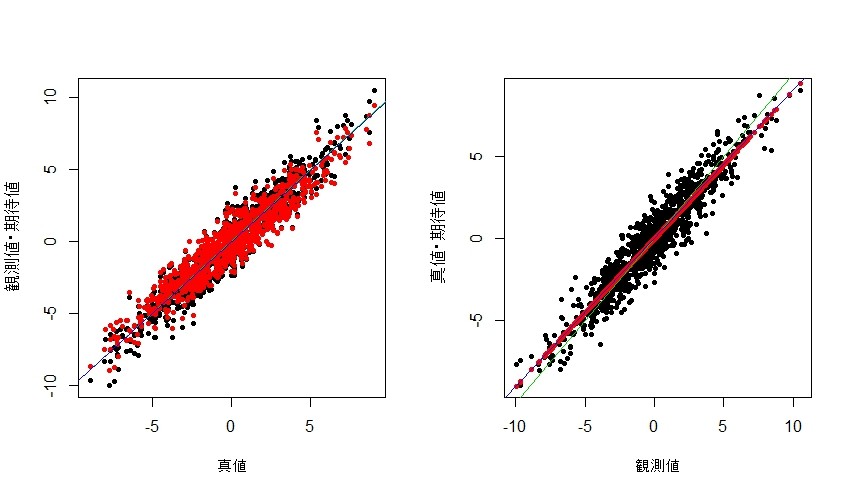
  • 図の左側は真値を横軸に、観測値(黒)と条件付き期待値(赤)を縦軸にとったもの。補助線は、切片0で傾き1の直線と、観測値~真値の線形回帰直線
  • 図の右側は観測値を横軸に、真値(黒)と条件付期待値(赤)を縦軸にとったもの。補助線は、切片0で傾き1の直線と、真値~観測値の線形回帰直線。観測値に基づく真値の回帰直線が、条件付期待値とほぼ一致しているのに対して、切片0で傾き1の直線(この直線は観測値そのものを期待値とした場合の線)が回帰直線とずれていることとを示している

# Xの真値
n <- 1000
d <- 3
X <- rnorm(n,0,d)
# 誤差項
s <- 1
Z <- rnorm(n,0,s)
# 観測値
Y <- X + Z
# 条件付期待値
X. <- d^2/(d^2+s^2)*Y

par(mfcol=c(1,2))
plot(X,Y,pch=20,xlab="真値",ylab="観測値・期待値")
points(X,X.,pch=20,col=2)
abline(0,1,col=3)
lm.out <- lm(Y~X)
lm.out
abline(lm.out[[1]][1],lm.out[[1]][2],col=4)

plot(Y,X,pch=20,xlab="観測値",ylab="真値・期待値")
points(Y,X.,pch=20,col=2)
abline(0,1,col=3)

lm.out2 <- lm(X~Y)
lm.out2
abline(lm.out2[[1]][1],lm.out2[[1]][2],col=4)
par(mfcol=c(1,1))

相互に関連した乱数

共分散行列 主成分分析 固有値分解
  • n個の正規乱数が、平均はすべて0で、covariance matrix \Sigmaに従って得られるとき、地道に自分で作れば、適当な正の正方行列を作って、その固有値分解をして正規直交基底方向の拡大縮小成分と回転成分とに分けておき、多次元標準正規乱数から拡大縮小と回転とをさせることで作成できる
  • やってみよう
# 変数の数
n <- 4
library(GPArotation)
V <- Random.Start(n)
S <- diag(runif(n)*5)
sigma <- V%*%S%*%t(V)
#sigma <- matrix(c(4,2,2,3), ncol=2)
#sigma <- matrix(runif(n^2),ncol=n)
#sigma <- sigma+t(sigma)
# その固有値分解
eigen.out <- eigen(sigma)
eigen.out[[1]]
# 変数n個の正規乱数のベクトルをn.setセット作る
n.set <- 1000
X <- matrix(rnorm(n.set*n),ncol=n)
#plot(as.data.frame(X),xlim=range(X),ylim=range(X))
# 拡大縮小する
X. <- t(t(X) * sqrt(eigen.out[[1]]))
#plot(as.data.frame(X.),xlim=range(X.),ylim=range(X.))
# 回転する
X.. <- t(eigen.out[[2]] %*% t(X.))
plot(as.data.frame(X..),xlim=range(X..),ylim=range(X..))
# パッケージを読み込んでrmvnorm()を使ってみる
library(mvtnorm)
x <- rmvnorm(n=n.set, mean=rep(0,n), sigma=sigma)
colMeans(x)
colMeans(X..)
var(x)
var(X..)

# 別法
x <- rmvnorm(n=n.set, mean=rep(0,n), sigma=sigma, method="chol")
colMeans(x)
var(x)
  • このような乱数に、相互に独立した観測誤差を入れる
  • 相互に共分散行列で関係付いた乱数は回転してやれば相互に独立した正規乱数として扱えるし、その回転において、観測誤差の間には関連が発生しないことを利用して、以下のようにして、観測結果から条件付期待値を算出してやることができる
  • やってみよう。上段は真値を横軸に、観測値・期待値とを縦軸にとった。下段は観測値を横軸に、真値・期待値を縦軸にとった。n個の乱数のうち3個を示したが、いずれも、真値~観測値の回帰直線と、条件付期待値との重なりがよいことが示されている

# 変数の数
n <- 4
library(GPArotation)
V <- Random.Start(n)
S <- diag(runif(n)*5)
sigma <- V%*%S%*%t(V)
#sigma <- matrix(c(4,2,2,3), ncol=2)
#sigma <- matrix(runif(n^2),ncol=n)
#sigma <- sigma+t(sigma)
# その固有値分解
eigen.out <- eigen(sigma)
eigen.out[[1]]
# 変数n個の正規乱数のベクトルをn.setセット作る
n.set <- 500
X <- matrix(rnorm(n.set*n),ncol=n)
#plot(as.data.frame(X),xlim=range(X),ylim=range(X))
# 拡大縮小する
X. <- t(t(X) * sqrt(eigen.out[[1]]))
#plot(as.data.frame(X.),xlim=range(X.),ylim=range(X.))
# 回転する
X.. <- t(eigen.out[[2]] %*% t(X.))
plot(as.data.frame(X..),xlim=range(X..),ylim=range(X..))

#########
# 上記の方法で発生させた共分散ありの多変数データをXに置きなおす
X <- X..
# 観測誤差は全変数で共通の正規乱数
s <- 1
Z <- rnorm(length(X..),0,s)
# 観測値
Y <- X + Z

# 観測値ありの下での条件付期待値は、共分散行列の固有値分解後の対角行列を
# 固有値そのままにするのは、「観測値そのものを期待値とする」ことに相当するが
# 条件付期待値の場合は、その分散を(真値の分散)/(真値の分散＋観測誤差の分散)ni
とすることなので、結局、固有値をその比で調整することが多変量化に相当する
X. <- t(eigen.out[[2]] %*% diag(eigen.out[[1]]/(eigen.out[[1]]+s^2)) %*% t(eigen.out[[2]]) %*% t(Y))

par(mfcol=c(2,3))
for(i in 1:3){


plot(X[,i],Y[,i],pch=20,xlab="真値",ylab="観測値・期待値")
points(X[,i],X.[,i],pch=20,col=2)
abline(0,1,col=3)
lm.out <- lm(Y[,i]~X[,i])
lm.out
abline(lm.out[[1]][1],lm.out[[1]][2],col=4)

plot(Y[,i],X[,i],pch=20,xlab="観測値",ylab="真値・期待値")
points(Y[,i],X.[,i],pch=20,col=2)
abline(0,1,col=3)

lm.out2 <- lm(X[,i]~Y[,i])
lm.out2
abline(lm.out2[[1]][1],lm.out2[[1]][2],col=4)
}

par(mfcol=c(1,1))

James Stein 推定から非線形Shrinkageへ

James Stein推定 Shrinkage
  • 複数の観測があるときに、それぞれの観測値の真値推定をするにあたり、観測値そのものにするより、「複数の観察を眺め渡して、そのばらつき・広がりより、少しきゅっと縮めた」値にしておく方がよいことが示せる
  • その「きゅっと縮める」ことをShrinkageと言い、縮め方の一つのやり方がJames Stein 推定法
  • この「きゅっと縮める」法がよいことを示しているのは、「全観測値にわたっての当てはまりのよさ」がよりよいことを示す不等式が得られることで示されるのだが、この「不等式」がOracle inequality。「え、言われるまで気づかなかったけど、自然の摂理な不等式ね」という意味合いだろうか。
  • じゃあ、どういう風にShrinkageするか、その最適化は、という問題が生じる
    • James Stein推定は、値ごとにShrinkageの程度を変えるので、「非線形」に見えるけれど、そのShrinkageの程度の計算自体は「線形」な方法
    • 「線形」なので、「非線形で素敵なもの」が見つかるなら、James-Steinを含めた、「実質的には線形な方法」より良いものがあるだろう
  • 関数(のパラメタ)を指定する空間での最適解探索をフーリエ変換のスペクトル探索と同じ道具立てにする。関数空間がソボレフ空間。スペクトル探索にするときに、部分空間に分けるらしいのだが、それは区間という部分空間に分けることに対応していて、それっていうのは調和解析がやってきたこと。そういう流れで、調和解析につながってくる

logo

図書室

日記全体の目次
(記事一覧)

疾患遺伝子解析を学ぶためのカタログ(H18 3月改訂)の目次

 教科書

京都大学大学院医学研究科集中講義 全８限Part I(2007)
京都大学大学院医学研究科集中講義 全８限Part II(2008)
京都大学大学院医学研究科統計遺伝学講義 全８限(2009)

以下の関連サイトへのリンク道案内ページ
遺伝子多型解析Wiki
東大医科研HGCゲノム機能解析分野(旧)
理研リウマチチーム解析資料ページ


疾患遺伝子解析を学ぶためのカタログ(H18 3月改訂)
遺伝統計学のための統計学基礎 全９限
Haploviewを用いた連鎖不平衡マッピング解析実習 全９限
Arlequinを用いた集団遺伝学実習 全７限
一から始める遺伝子多型・形質関連解析
多数のGWAS/GWASメタアナリシスとその周辺解析用のアプリケーションへのリンク

複合遺伝性疾患とは

----------News----------
20万アクセス
2008/07/20
40万アクセス
2010/09/12


-------------------------