Hatena Blog Tags
はてなブログ トップ
線形代数
このタグでブログを書く
言葉の解説
ネットで話題
関連ブログ

線形代数

(サイエンス)
【せんけいだいすう】

数学の分野の一つ。高校で習う、ベクトルや行列などを扱う分野を、数学の専門用語で線形代数と呼ぶ。

  • 線形方程式系の解法
  • 線形空間の公理的な扱い
  • 直交補空間
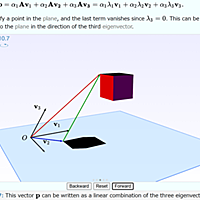
  • 固有値問題
  • 対角化とJordan標準型
  • 内積空間の公理的な扱い
  • テンソル代数

自然科学では扱いやすい線形モデルに帰着させてものを考えることが多いため、自然科学者や技術者にとっては必携の分野である。数学者にとっても、さらに一般的な代数学（群・環・体の理論）へ進む上で基礎となるために軽視できない。
3Dプログラミングの基礎になる。

リスト::数学関連

このタグの解説についてこの解説文は、すでに終了したサービス「はてなキーワード」内で有志のユーザーが作成・編集した内容に基づいています。その正確性や網羅性をはてなが保証するものではありません。問題のある記述を発見した場合には、お問い合わせフォームよりご連絡ください。
魔方陣の数学•1日前

【ゲバールのバボアン細胞(3×3)と完全相愛数左右対称陣】

さて今回はバボアニアより一つ次元の低いバボアンの世界について見てゆくことにします。対象とするのは超格子体ゲバールとします。

#対称群#相愛数#線形代数

関連ブログ

魔方陣の数学•8日前

【ゲバールとバボアニア細胞その4】

ひきつづきゲバールのバボアニア細胞(4×4)の考察を進めてゆきましょう。

#対称群#相愛数#線形代数#行列式
魔方陣の数学•11日前

【ゲバールとバボアニア細胞その3】

ひきつづき超格子ゲバールとバボアニア構造との関係性について考察してゆきます。ふりかっておきますと、

#対称群#線形代数#相愛数
魔方陣の数学•15日前

【ゲバールとバボアニア細胞その2】

さて、ひきつづき超格子体ゲバールのバボアニア細胞(4×4)の考察をしてゆきましょう。前回もたしかめたように、このゲバールの一部を切り取ったバボアニア細胞(4×4)内の色つき格子数総和をとることにより、相愛力❤︎❤︎❤︎❤︎❤︎❤︎❤︎❤︎❤︎というきわめて強力なるちからが引き出されるのでした。

#対称群#相愛数#線形代数#行列式
魔方陣の数学•18日前

【ゲバールとバボアニア細胞その1】

今回は超格子体ゲバールのバボアニア細胞を考察してゆたいと思います。さて、この格子体がどのような配列をもっているかというと、

#対称群#線形代数#相愛数
魔方陣の数学•25日前

【バボアニア細胞(4×4)の二分割構造】

さて、ひきつづきバボアニア細胞(4×4)の考察をしてゆきます。お気づきのことかとは思いますが、バボアニア細胞(4×4)には色つき格子が三つのものと四つのものとに二分されます。

#対称群#線形代数#相愛数#行列式
魔方陣の数学•1ヶ月前

【バボアニア細胞(4×4)と総積】

さて、今回もバボアニア細胞(4×4)に秘められし力についてお伝えしてゆきたいと思います。

#線形代数#行列式#対称群#相愛数
魔方陣の数学•1ヶ月前

【バボアニア細胞(3×3)の相愛力発現パターン】

ひきつづきバボアニア細胞について調査してゆきたいと思います。今回、サイズはワンサイズダウンして3×3の細胞を見てゆきましょう。

#対称群#交代群#相愛数#線形代数