FreeCADで動くPythonスクリプト その3(法線ベクトル)
今回はFreeCADで法線ベクトル(normal vector)を表示させるPythonスクリプトを説明します
前提条件として
FreeCAD上で定義された面(Face)を対象とします
SolidやShell等を構成するFaceを選択した状態でも動作します
FreeCADのv0.20でしか動作検証してません
# Get normal vector of a face of Selected-Object import Draft def norm(a, b, c=0): """ Return norm of argument numbers """ return (a**2 + b**2 + c**2)**(1/2) def plot_line(vector_a, vector_b): """ Plot line from argument vectors """ line = Draft.make_line(vector_a, vector_b) Draft.autogroup(line) # Not required after version 0.19? # Get Selected-Objects to obj obj = FreeCADGui.Selection.getSelection() if len(obj): shp = obj[0].Shape # Get shp as shape from obj if shp.ShapeType != "Face": # Get Selected-SubObject to shp shp = FreeCADGui.Selection.getSelectionEx()[0].SubObjects[0] CoM = shp.CenterOfMass BBx = shp.BoundBox length_axis = norm(BBx.XMax-CoM.x, BBx.YMax-CoM.y, BBx.ZMax-CoM.z) Normal = shp.normalAt(0, 0) # Normal vector plot_line(CoM, CoM + length_axis*Normal) FreeCAD.Console.PrintMessage("Normal {}\n".format(Normal)) else: FreeCAD.Console.PrintMessage("-------- No valid setected object! --------\n")
【表示項目】
Normal Vector 法線ベクトル(X, Y, Z)(mm)
【使い方】
・対象となる面を選択した状態で本スクリプトを実行してください
・何も選択していない状態で実行するとWarningが表示されます
・正常に実行されればReport viewに法線ベクトル成分が出力されます
・モデルビューに法線ベクトルを表す線分が描画されます
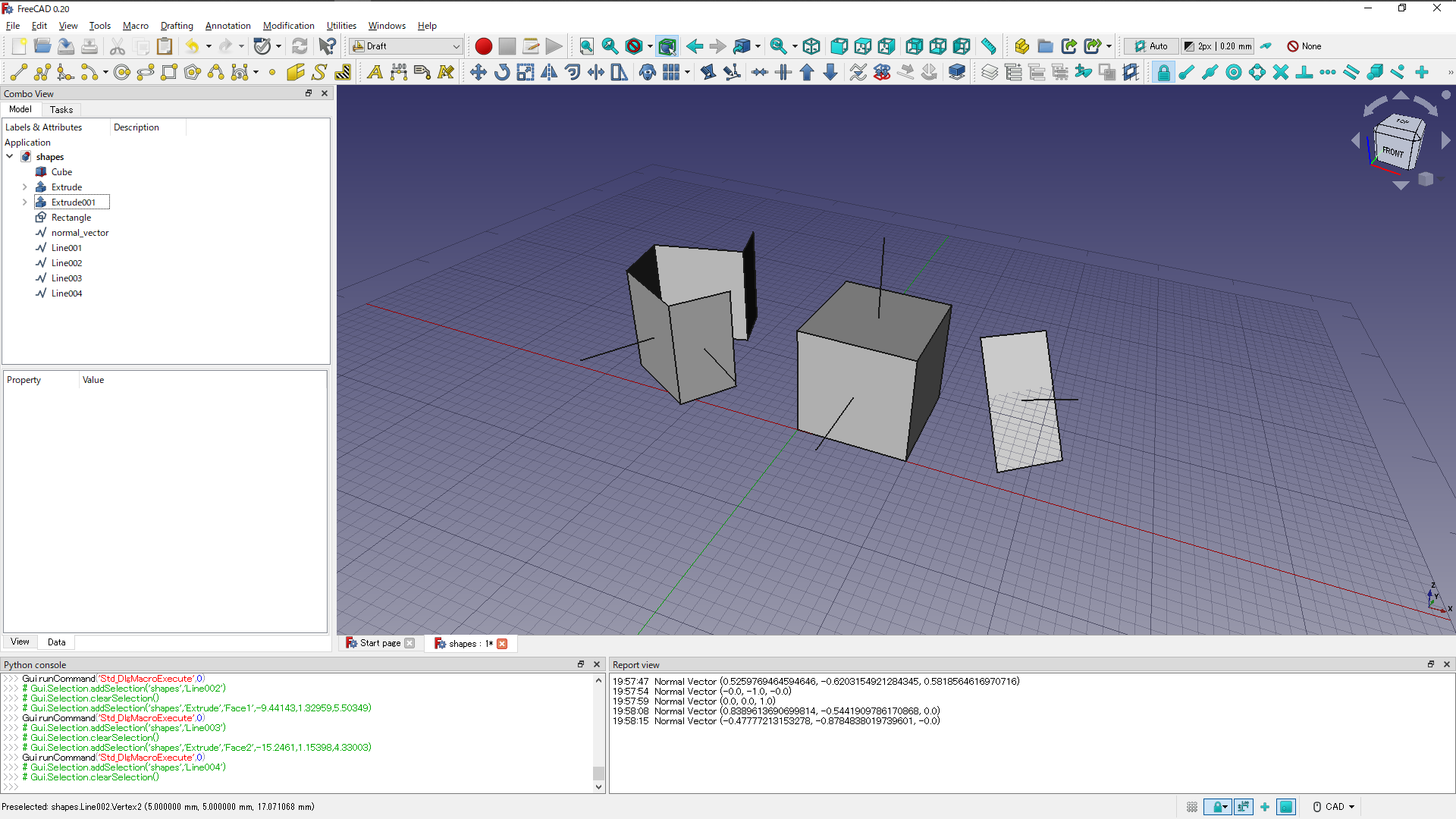
FreeCADで具体的な面に適用した例を示します
FreeCADで動くPythonスクリプト その2(重心・質量中心)
今回はFreeCADで重心・質量中心を表示させるPythonスクリプトを説明します
前提条件として
FreeCAD上で定義された単一の形状(Shape)を対象とします
"重心"はShapeが持つPropertyの"CenterOfGravity"の値を参照しています
"質量中心"はSubShapes(Shapeの構成要素)が持つPropertyの"CenterOfMass"の値を集計したものとなります
材質はすべて均一なものを想定し,重みを評価していません
FEMワークベンチでMaterialSolidを定義していも参照はされない仕様の様です
FreeCADのv0.20でしか動作検証してません
# Properties of Shapes # Show ShapeType, Number of SubShapes, Area, Volume and Center of gravity, # Calcurate Mass and Center of mass of Selected-Objects # Shapes should be grouped into a single object. import Draft def total_mass(shape, a=0): """ Calcurate Mass and Center of mass of argument shape """ M = 0 xx = FreeCAD.Vector(0, 0, 0) for i in range(len(shape.SubShapes)): st = shape.SubShapes[i].ShapeType ms = shape.SubShapes[i].Mass cm = shape.SubShapes[i].CenterOfMass M += ms xx += ms*cm if a: # a != 0 -> output breakdown of total mass FreeCAD.Console.PrintMessage("%d, %s, %f, %f, %f, %f\n" % (i, st, ms, cm.x, cm.y, cm.z)) CoM = xx/M return M, CoM def plot_point(vector_a): """ Plot point from argument vector """ point = Draft.make_point(vector_a) Draft.autogroup(point) # Not required after version 0.19? # Get Selected-Objects to obj obj = FreeCADGui.Selection.getSelection() if len(obj): shp = obj[0].Shape # Get shp as shape from obj FreeCAD.Console.PrintMessage("-------- Properties of Shapes --------\n") # Show ShapeType of shp FreeCAD.Console.PrintMessage("ShapeType = %s\n" % shp.ShapeType) # Show Number of faces, shells, solids and subshapes in shp FreeCAD.Console.PrintMessage("Number of faces, shells, solids, subshapes = %d, %d, %d, %d\n" \ % (len(shp.Faces), len(shp.Shells), len(shp.Solids), len(shp.SubShapes))) # Show Area of shp FreeCAD.Console.PrintMessage("Area = %f\n" % shp.Area) # Show Volume of shp FreeCAD.Console.PrintMessage("Volume = %f\n" % shp.Volume) # Show Center of gravity of shp CoG = shp.CenterOfGravity FreeCAD.Console.PrintMessage("Center of gravity = (%f, %f, %f)\n" % (CoG.x, CoG.y, CoG.z)) # Calcurate Mass and Center of mass M, CoM = total_mass(shp) FreeCAD.Console.PrintMessage("Mass = %f\n" % M) FreeCAD.Console.PrintMessage("Center of mass = (%f, %f, %f)\n" % (CoM.x, CoM.y, CoM.z)) # Plot point as Center of gravity plot_point(CoG) FreeCAD.ActiveDocument.Point.Label = "center_of_gravity" # Plot point as Center of mass plot_point(CoM) FreeCAD.ActiveDocument.Point001.Label = "center_of_mass" FreeCAD.ActiveDocument.recompute() else: FreeCAD.Console.PrintMessage("-------- No valid setected objects! --------\n")
【表示項目一覧】
ShapeType Shapeの種別 Number of faces... Shapeの内訳(face, shell, solid, subshapeの個数) Area 断面積(mm2) Volume 体積(mm3) Center of gravity 重心(X, Y, Z)(mm) Mass 質量* Center of mass 質量中心(X, Y, Z)(mm)
※単位面積質量1として
【使い方】
・対象となる形状を選択した状態で本スクリプトを実行してください
・何も選択していない状態で実行するとWarningが表示されます
・正常に実行されればReport viewに重心・質量中心が出力されます
・モデルビューに重心と質量中心を表す点が描画されます
FreeCADで具体的な形状(高さ10 mmの円錐)に適用した例を示します

ShapeTypeが"Solid"なので重心はSolidモデルとしての値が表示されます
一方でSubShapesは"Shell"が1つなので質量中心はShellモデルとしての値が表示されます
【追記】
円錐の重心位置を一応確認しておきます
center_of_gravity_of _cone.wxm

半径r,高さhの円錐の任意高さxにおける断面積Aは%o1式で表されます
上式を0~hの区間で積分した結果を体積Vとして%o2式に示します
%o1式に重みxをかけて積分した結果を1次モーメントSとして%o3式に示します
S/Vを計算した結果を重心高さgとして%o4式に示します
ということで,重心高さ 10/4 = 2.5 mm でスクリプトの値と一致していますね(*´ω`*)
FreeCADで動くPythonスクリプト その1(断面性能)
今回はFreeCADで断面性能を表示させるPythonスクリプトを説明します
AutoCADにはリージョンの断面性能を表示させるマスプロパティ(MASSPROP)というコマンドがあります
複雑な断面形状の図心位置や断面2次モーメント等を知りたいとき大変重宝する機能ですね
これと同じ様なことをFreeCADでもやりたいというお話です(*´ω`*)
前提条件として
FreeCAD上で定義された単一の面(Face)を対象とします
XY平面,XZ平面, YZ平面のいずれかに平行に配置されていることを想定しています
FreeCADのv0.20でしか動作検証してません
# Properties of Section # Show Area, Length, Boundary, Center of mass, Second moment of area, Product of inertia, # Radius of gyration, Principal moments of inertia, Principal axes and Section modulus of Selected-Object # Section must be located on a Cartesian coordinate plane. import Draft def norm(a, b, c=0): """ Return norm of argument numbers """ return (a**2 + b**2 + c**2)**(1/2) def section_modulus(shape): """ Calculate Section modulus from argument shape """ BBx = shape.BoundBox CoM = shape.CenterOfMass # Calculate distance from the neutral axis to the most extreme fibre x1 = abs(BBx.XMax - CoM.x) x2 = abs(BBx.XMin - CoM.x) y1 = abs(BBx.YMax - CoM.y) y2 = abs(BBx.YMin - CoM.y) z1 = abs(BBx.ZMax - CoM.z) z2 = abs(BBx.ZMin - CoM.z) MoI = shape.MatrixOfInertia Ixx = MoI.A11 Iyy = MoI.A22 Izz = MoI.A33 Z1 = FreeCAD.Vector(Ixx/norm(y1, z1), Iyy/norm(x1, z1), Izz/norm(x1, y1)) Z2 = FreeCAD.Vector(Ixx/norm(y2, z2), Iyy/norm(x2, z2), Izz/norm(x2, y2)) return Z1, Z2 def plot_point(vector_a): """ Plot point from argument vector """ point = Draft.make_point(vector_a) Draft.autogroup(point) # Not required after version 0.19? def plot_line(vector_a, vector_b): """ Plot line from argument vectors """ line = Draft.make_line(vector_a, vector_b) Draft.autogroup(line) # Not required after version 0.19? def plot_principal_axes(shape): """ Plot principal axes from argument shape """ BBx = shape.BoundBox CoM = shape.CenterOfMass length_axis = norm(BBx.XMax-CoM.x, BBx.YMax-CoM.y, BBx.ZMax-CoM.z) I_eivect1 = shp.PrincipalProperties.pop("FirstAxisOfInertia") I_eivect2 = shp.PrincipalProperties.pop("SecondAxisOfInertia") I_eivect3 = shp.PrincipalProperties.pop("ThirdAxisOfInertia") # FreeCAD.Console.PrintMessage("Principal axis 1 = {}\n".format(I_eivect1)) # FreeCAD.Console.PrintMessage("Principal axis 2 = {}\n".format(I_eivect2)) # FreeCAD.Console.PrintMessage("Principal axis 3 = {}\n".format(I_eivect3)) plot_line(CoM, CoM + length_axis*I_eivect1) plot_line(CoM, CoM + length_axis*I_eivect2) plot_line(CoM, CoM + length_axis*I_eivect3) # Get Selected-Object to obj obj = FreeCADGui.Selection.getSelection() if len(obj): shp = obj[0].Shape # Get shp as shape from obj # Show Area of shp FreeCAD.Console.PrintMessage("-------- Properties of Section --------\n") FreeCAD.Console.PrintMessage("Area = %f\n" % shp.Area) # Show Length of shp FreeCAD.Console.PrintMessage("Length = %f\n" % shp.Length) # Show Boundary box of shp BBx = shp.BoundBox FreeCAD.Console.PrintMessage("Boundary box = (%f, %f, %f, %f, %f, %f)\n" % \ (BBx.XMin, BBx.XMax, BBx.YMin, BBx.YMax, BBx.ZMin, BBx.ZMax)) # Show Center of mass of shp CoM = shp.CenterOfMass FreeCAD.Console.PrintMessage("Center of mass = (%f, %f, %f)\n" % (CoM.x, CoM.y, CoM.z)) # Show Second moment of area and Product of inertia of shp MoI = shp.MatrixOfInertia FreeCAD.Console.PrintMessage("Second moment of area = (%f, %f, %f)\n" % (MoI.A11, MoI.A22, MoI.A33)) FreeCAD.Console.PrintMessage("Product of inertia = (%f, %f, %f)\n" % (MoI.A12, MoI.A13, MoI.A23)) # Show Radius of gyration Rg = shp.PrincipalProperties.pop("RadiusOfGyration") FreeCAD.Console.PrintMessage("Radius of gyration = {}\n".format(Rg)) # Show Principal moments of inertia and Principal axes I_eivals = shp.PrincipalProperties.pop("Moments") FreeCAD.Console.PrintMessage("Principal moments of inertia = {}\n".format(I_eivals)) # Plot point as Center of mass plot_point(CoM) FreeCAD.ActiveDocument.Point.Label = "center_of_mass" # Plot lines as Principal axes plot_principal_axes(shp) FreeCAD.ActiveDocument.Line.Label = "principal_axis_1" FreeCAD.ActiveDocument.Line001.Label = "principal_axis_2" FreeCAD.ActiveDocument.Line002.Label = "principal_axis_3" FreeCAD.ActiveDocument.recompute() # Calculate Section modulus Z1, Z2 = section_modulus(shp) FreeCAD.Console.PrintMessage("Section modulus = (%f, %f, %f, %f, %f, %f)\n" % \ (Z1.x, Z2.x, Z1.y, Z2.y, Z1.z, Z2.z)) else: FreeCAD.Console.PrintMessage("-------- No valid setected object! --------\n")
※主軸ベクトル(I_eivect1~3)を表示させる箇所はコメントアウトしてます
【表示項目一覧】
Area 断面積(mm2) Length 周長(mm) Boundary box 境界枠(X1, X2, Y1, Y2, Z1, Z2)(mm) Center of mass 図心(X, Y, Z)(mm) Second moment of area 断面2次モーメント(Ixx, Iyy, Izz)(mm4) Product of inertia 慣性乗積(Ixy, Ixz, Iyz)(mm4) Radius of gyration 回転半径(R1, R2, R3)(mm) Principal moments of inertia 主慣性モーメント(I1, I2, I3)(mm4) Section modulus 断面係数(Zx1, Zx2, Zy1, Zy2, Zz1, Zz2)(mm3)
※断面2次モーメントは図心を通り座標系に平行な各軸回りの値となります
(AutoCADのMASSPROPではワールド座標系の各軸回りの値となっており,挙動が異なるので注意してください)
【使い方】
・対象となるフェースを選択した状態で本スクリプトを実行してください
・何も選択していない状態で実行するとWarningが表示されます
・正常に実行されればReport viewに断面性能が出力されます
・モデルビューに図心を表す点と主軸ベクトルを表す線分が描画されます
FreeCADで具体的な断面に適用した例を2つ示します
矩形断面(50x100)

不等辺山形断面(L200x90x8/14)

FreeCADで4辺単純支持板の計算(固有振動数)
今回はFreeCADでモデル化した4辺単純支持板の固有値解析例を紹介します
平板の形状寸法は 短辺長さa=500 mm,長辺長さb=1,000 mm,板厚h=10 mm です
材質はSS400相当とします
まずは板理論を使って1次振動モードの固有振動数を計算します
frequency_simply-plate2.wxm

4辺単純支持板の1次の固有振動数の算式を%o1に示します(式の導出については"4辺単純支持板の固有振動数"を参照ください)
単位体積重量γと単位体積質量ρの関係式を%o2に示します
上式で%o1式を書き直した結果を%o3に示します

板の曲げ剛性Dの計算式を%o4に示します

形状寸法 a=500 mm,b=1,000 mm,h=10 mm,ヤング率E=210,000 N/mm2,単位体積質量ρ=7.8*10^-9 ton/mm3 をそれぞれ代入します(画面出力は省略)
板の曲げ剛性Dを計算した結果を%o11に示します(単位はN.mm)
弱軸方向の1次振動モードの固有振動数Nを計算した結果を%o12に示します(単位はHz)
FreeCADのFEMワークベンチによる固有値解析結果
メッシングにはGmsh,ソルバーにはCalculiXを使用しています
2Dのサーフェースモデル(plate_2d.FCStd)

変位量プロット(変位分布が振動モードを表しますが,大きさに意味はありません)
1次の固有振動数 122.78 Hz
3Dのソリッドモデル(plate_3d.FCStd)

変位量プロット(変位分布が振動モードを表しますが,大きさに意味はありません)
1次の固有振動数 181.06 Hz
ということで,FreeCADによる4辺単純支持板の固有値解析例を紹介しました
FreeCADで片持ち梁の計算(固有振動数)
今回はFreeCADでモデル化した片持ち梁の固有値解析例を紹介します
片持ち梁のモデルはFreeCADで片持ち梁の計算(静的応力解析)と全く同様です
まずは梁理論を使って1次振動モードの固有振動数を計算します
frequency_cantilever3.wxm

片持ち梁の1次の固有振動数の算式を%o1に示します(式の導出については"片持ち梁の固有振動数 その2"を参照ください)
単位体積重量γと単位体積質量ρの関係式を%o2に示します
上式で%o1式を書き直した結果を%o3に示します

断面積Aの計算式を%o4に示します
断面2次モーメントIの計算式を%o5に示します
【弱軸方向】

形状寸法 B=100 mm,D=50 mm,L=1,000 mm,ヤング率E=210,000 N/mm2,単位体積質量ρ=7.8*10^-9 ton/mm3 をそれぞれ代入します(画面出力は省略)
断面積Aを計算した結果を%o11に示します(単位はmm4)
断面2次モーメントIを計算した結果を%o12に示します(単位はmm4)
弱軸方向の1次振動モードの固有振動数Nを計算した結果を%o13に示します(単位はHz)
【強軸方向】

断面幅Bと断面深さDの値を入れ替えます(画面出力は省略)
断面2次モーメントIを計算した結果を%o16に示します(単位はmm4)
強軸方向の1次振動モードの固有振動数Nを計算した結果を%o17に示します(単位はHz)
FreeCADのFEMワークベンチによる固有値解析結果
メッシングにはGmsh,ソルバーにはCalculiXを使用しています
2Dのサーフェースモデル(beam_2d.FCStd)

変位量プロット(変位分布が振動モードを表しますが,大きさに意味はありません)
1次の固有振動数 42.03 Hz*
2次の固有振動数 83.37 Hz
※サーフェースモデルにElementGeometry2Dで板厚情報を付与していますので面外弱軸方向の固有振動数もちゃんと計算してくれます(*´ω`*)
3Dのソリッドモデル(beam_3d.FCStd)

変位量プロット(変位分布が振動モードを表しますが,大きさに意味はありません)
1次の固有振動数 42.04 Hz

変位量プロット(変位分布が振動モードを表しますが,大きさに意味はありません)
2次の固有振動数 83.45 Hz
ということで,FreeCADによる片持ち梁の固有値解析例を紹介しました
片持ち梁の固有振動数 その2
前回に引き続き,求めた片持ち梁のたわみ関数を使って固有振動数を計算してみます
Xmが変わっただけで,やってることは片持ち梁の固有振動数 その1と全く同じです
梁の長さを l,単純曲げ変形のみとし,E,A,I,γは一定とします
y : 梁のたわみ関数
Xt : 時間発展を表す関数
y が位置 x と時間 t の関数であること,Xt が t の関数であることをそれぞれ%o1, %o2式で宣言します(画面出力は省略)
連続体の梁の運動方程式を%o3式に示します
梁の運動方程式の導出については運動方程式とラグランジアン その4を参照ください

Xm : モードを表す関数
%o4式にて,y を x の関数と t の関数の積で表します(変数分離)
Xm に前回求めた片持ち梁の一次モードを表す式を代入します(%o5, 6)
上式を元の運動方程式に戻して計算した結果を%o7式に示します
上式が有意な解を持つための条件として%o8式が与えられます

Xt に, 角振動数がωとなる適当な調和振動関数を代入します(%o9)
上式を%o8式に戻して計算した結果を%o10式に示します
この方程式をωについて解いた結果を%o11式に示します
solve:以下の文言は目に見える解だけが全てではないと我々に警告してくれています,ありがたいことです('A`)
固有振動数 N とωの関係式を%o12式に示します
上式に%o11式を代入してまとめた結果を%o13式に示します
ということで,片持ち梁の一次の固有振動数が得られます
追記

以前適当な調和関数で求めた固有振動数をN1,今回求めた固有振動数をN3としてN1/N3を%o15に示します
凡そ30%程度と結構な差がありますねー('A`)
振動する梁のたわみ関数 その3
以前,片持ち梁の固有振動数を求める際に一次モードの梁のたわみ関数を与えましたが
簡単な調和振動関数を前提としたもので精度はそれなりでした。
今回はもう少しちゃんと計算をしたら?というお話です
%i1にてパッケージ"newton1"をロードします(画面出力は省略)
newton1はニュートン法を利用するためのパッケージです(ニュートン法 その1を参照ください)
梁のたわみ関数y(x)を任意の調和振動関数(%o2)で仮定します
振動する梁のたわみ関数 その1に比べて係数CとDの項が増えてます
【片持ち梁】

片持ち梁の境界条件を指定します(係数が2つ増えたので境界条件も2つ増えてます)
- x = 0 の位置の変位が 0 (%o3)
- x = 0 の位置のたわみ角が 0 (%o4)
- x = l の位置の曲率が 0 (%o5)
- x = l の位置の3階微分が 0 (%o6)
上4式を未定係数A~Dに対しての連立方程式として,係数マトリックスを%o7式に示します
係数マトリックスの特異性より%o8式を得ます
この方程式を ω*l について解きたいのですが残念ながら陽には解けません
仕方ないのでニュートン法を使って求めた(1次の振動モードに対応する)数値解を%o9式に示します
1次以外の数値解を求めたい場合は初期値(x0 = 2)を別の値へ修正してください
余談ですがこの ω*l を固有値と呼びます

係数マトリックスと未定係数ベクトルの積を%o9式でまとめた結果が%o11式となります
上式の2~4成分を連立方程式としてB~Dについて解いた結果を%o12式に示します
この解で%o2式を書き直したものを%o13式に示します(Aは任意の振幅)

数値解を用いたたわみ関数y3は見た目でどんな曲線なのか全然分からないですね
比較のため振動する梁のたわみ関数 その1で求めたたわみ関数をy1として%o14式に示します
y1を赤線,y3を青線で%t15にプロットします
重ねてみると割と差がある様な気がしないでもないですね(´・ω・)

