オーストラリアコンベンション 3日目
コンベンション自体は2日目(タイトルまぎらわしい)
ORI-REVOを使ったワークショップを午前と午後の2回実施。
1回2時間。10名。各自のノートPCでORI-REVOのページにアクセスして、好みの形を作成。データをメールで送ってもらって、カッティングプロッタ CAMEO で折り筋加工。
思いのほか、参加者の皆さん慎重で、データを送る前に、実際に上手にできるかどうかを時間をかけて検証していた様子。そんなに無理な形を作っていることはなかった。Chrome book, iPad で、ORI-REVOが動作しなかったのは残念。
今回も全体的には、幾何学的な形を対象としたワークショップが多かった印象。
夕方のイベントでは、90cm四方の大きな紙での折紙制作。折り紙本などのオークション。
その後、皆で片づけをして、無事にイベント終了。
わずか2日間だけだったけれど、準備、運営は本当に大変だったと思う。私に対する気遣いもたくさんしてもらって、本当に恐縮。感謝。
ご年配の方々が旧交を温めている一方で、平坦折りのNP困難の話や、折紙でNANDゲートを作る話、Hyperbolic projection で展開図を作る話などの、コンピュータサイエンスや数学の話をしている理工系の若手がいて、そのそばを子どもたちがかけまわっている、なんとも不思議な和やかな空間でした。
オーストラリアコンベンション2日目
ホテルから会場までは歩いて10分ほど。
9時ごろに会場について展示作品のセットアップ。
他の方々の作品も。Winnieさんの曲線折りの作品を中心に、Tessellation、ユニットなど、全体的に幾何学的なものが多い印象。
10時半から90分間、講演と曲線折りのワークショップを担当。40名程度の参加。
会場に隣接しているショッピングセンターで、昼食を購入。セルフレジでクレジットカードを使えるので簡単便利。
午後、他のワークショップに参加。Hans Werner-Guth の Jum Orbを作ったり。円弧を不要になったCD-ROMを使って描くのは斬新。キッチンペーパーに、絵の具や水糊などを使って、オリジナルの紙づくりをするワークショップも新鮮だった。
夕方、折紙イベント。片手での折り鶴早折り競争。2人ずつのペアで、それぞれ片手を使っての鶴の早折り競争。3回の折りだけで作る作品コンテスト。
そのあと、折り紙作家5名が登壇してのパネルディスカッション。会場からの質問が多数。興味深いものも多かった。
・折り紙創作で生活していくためのお金を稼ぐことの難しさ
・自分で何か新しいものを作ったと思っても、「それは以前に○○さんが作ったのと同じだ」と指摘されることが多くて、意欲をくじかれることが多い
・折紙創作のインスピレーション、アイデアはどのように得ることが多いか
・将来に対してどのような展望をもっているか
・参考となる書籍はどれか
・折り図の作成はどのようにしているか
他にもたくさんの質問があって盛り上がった
オーストラリアは広くて(国内でも時差がある)、1つのまとまった組織としての運営が難しいというような話もあった。
とにもかくにも、イベントを取りまとめされているWinnieさんは大変そうだった。本当にお疲れさまです。
オーストラリアコンベンション1日目
8月11日夜、成田空港発の便でオーストラリア、ゴールドコーストへ。9時間弱のフライト。
ゴールドコーストに着いてみると、予定していたシドニーへの乗り継ぎ便がキャンセルになったとの連絡。5時間あとの便で移動することになって、結局7時間ほどゴールドコーストの空港で待機。
その後、無事にシドニーに到着。現地時間で午後4時過ぎ。
現地にて、Winnie Leungさん(シドニーコミュニティの代表)、Michael Assisさん(メルボルンコミュニティの代表)のお迎え。会場のHarold Park近くのホテルまで同行していただいて、ホテルにチェックイン。
自宅を出てからおよそ24時間で、どうにか目的地へ。日本との時差は1時間。
その後、同じホテルに宿泊される方々も一緒に夕食。アジア料理のお店(チキンフォーを食べた)。
この日のトラブル
・空港でのWiFiルータの受け取り時間を予約時に勘違いしていて、空港に着いたときには受け取り時間の枠を過ぎていた(別のターミナルの受付カウンターで受け取れた)
・手配していただいていた航空券のパスポート番号に間違いがあった
・予定していた乗り継ぎ便がキャンセルになった
トラブルはよくあること
メンガーのスポンジの紙工作

この形が結構気に入って、紙で作ったらカッコ良さそうな気がしたので作ってみました。
展開図はペパクラデザイナーですぐに作れます。
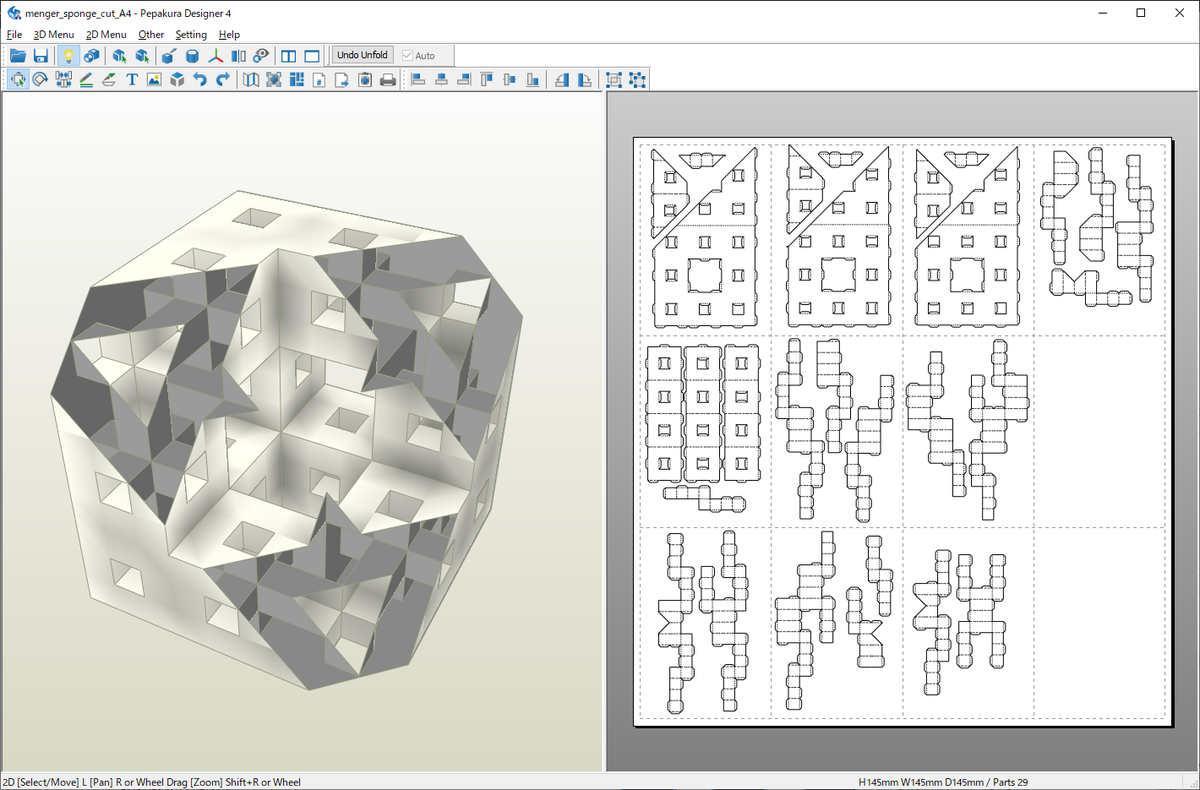
実際に作ってみました。

写真をもう少ししっかり撮ってみました。

組み立てるのが結構大変で、隙間ができてしまったり、細かいところがしっかり作れていません。たぶん、展開図にするときの分割の方法やのりしろの付け方に拠るのだと思います。
見えていない内部もしっかり作っているので、組み立てには時間がかかりました。
展開図を、ペパクラデザイナーの作品投稿ページで公開しています。
https://tamasoft.co.jp/pepakura/gallery/gallerydetails.php?id=1576
(続)メンガーのスポンジ
前回の記事のメンガーのスポンジの形はCGソフトでモデリングして作っていましたが、フラクタルのレベルを上げるたびに、その3乗のオーダーでデータ量が増えるので、前回作成したlevel4以上を作るのはあまり現実的でありません。
そこで、シェーダーを書いて、それ以上の詳細度を持つ形状表現ができるようにしてみました。
動画はこちら
実行ファイル、プログラムコードはこちらに置いてあります。
https://github.com/jun-mitani/menger-sponge/blob/master/README.md
シェーダーはレイマーチングを使っていて、基本的な考え方は、次のような感じ。
各画素単位でレイを飛ばして、物体にぶつかるまでの距離と、ぶつかった場所の法線を算出。その情報からピクセルの色を決定する。
このアプローチだと、処理にかかる時間やデータ量は主に画素数に依存して、フラクタルのレベルにはあまり依存しなくなります。
断面を求める計算も、平面上をレイの出発点とすればよいだけなので、簡単に実現できます。
メンガーのスポンジ
フラクタル図形として有名なものの1つに立方体に穴をあけて作る「メンガーのスポンジ」と呼ばれるものがあります。
詳しくはこちら。
次のツイートに触発されて、いろいろな画像を作ったので、ここで紹介します。
立方体をうまく切ると断面が正六角形になる。メンガーのスポンジで同じところを切ると、断面はどんな形になるだろう?
— 盛田みずすまし (@nosiika) 2020年4月18日
まず最初の基本立体(レベル1、穴の無いただの立方体がレベル0)。

つづいてレベル2

次がレベル3

次がレベル4

これらを平面で切断してみた様子。
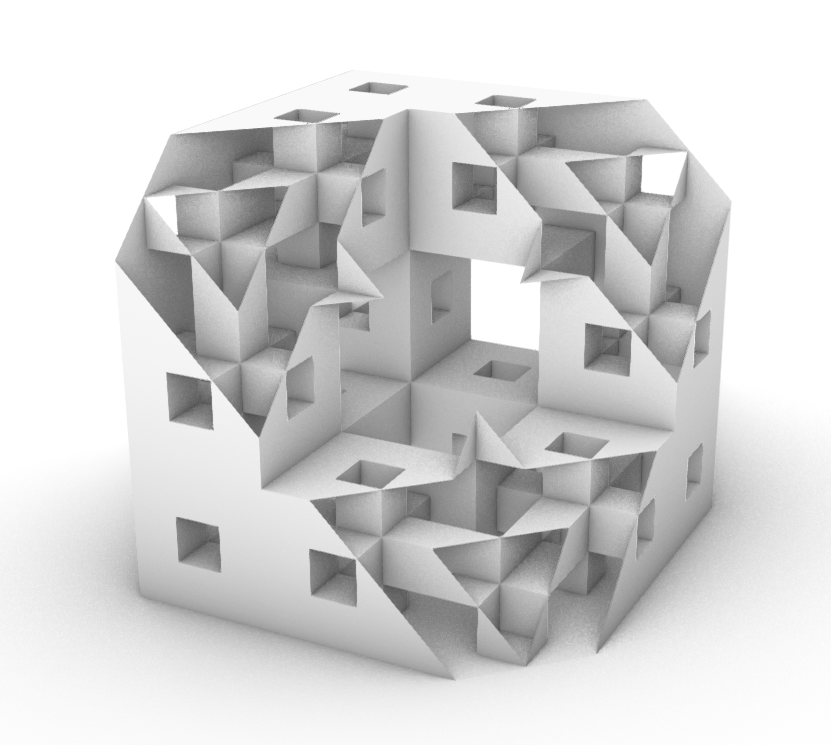

切断面が正六角形になるようにした様子。




中身の詰まったモデルだとすると。星の模様が見て取れます。


断面を正面から見た様子

文化交流使(56日目:ハノイ)
いよいよ今日が、文化交流使としての派遣期間最終日です。
午前に国際交流基金センターで講演とワークショップを行い、これまでの8週間にわたる勤めを無事に終えることができました。
ワークショップでは、現地のベトナム折り紙グループの方々が手伝ってくれたので、とても心強かったです。
これで、これまでの8週間、8か国12都市を訪問し、あとは日本への帰国を残すばかりとなりました。
当初は厳しいスケジュールだなぁと思い、いざ旅に出てみると、案の定、道半ばでは体調を崩し辛いこともありましたが、でも今になって振り返ると、やってできないことはない、ちょうどよい難易度の設定で、さすが文化庁、もしかして全部お見通しだったのではないかとさえ思えてしまいます。(本来は私自身でスケジュールを決めなくてはいけないところ、なかなか決めるのが難しかったので、文化庁よりご提案いただきました)
とくにバングラデシュ、インドは香辛料と油で胃腸をやられたように思いますが、この2か国がなかったら、たぶん平穏すぎたと思いますから、やっぱり行ってよかったと思います。日本とは大きく異なる文化、環境を肌で感じることができました。
全部で35回の講演・ワークショップを行い、約1900名の参加者に対して、折り紙の話をすることができました。
各会場でご挨拶し、お世話になった方々を含めると2000名を超えそうな感じです。
これまでに15回飛行機に乗り、12のホテルを渡り歩いてきました。
よく頑張ってきた気がします。この期間を通して、お会いした方々になにか少しでも残してくることができたなら、とても嬉しく思います。
まだ日本への移動が残っていますが、今回の派遣を支えてくれた皆さんに、こころ感謝申し上げます。
