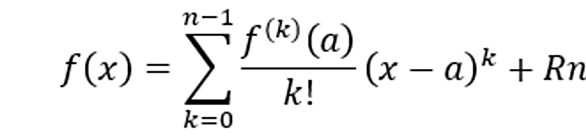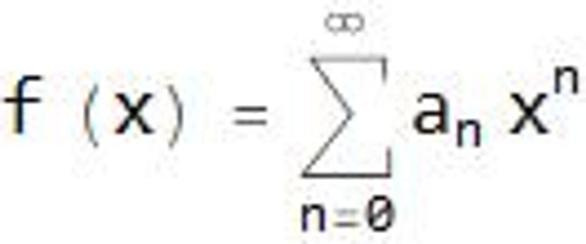Hatena Blog Tags
はてなブログ トップ
マクローリン展開
このタグでブログを書く
言葉の解説
ネットで話題
関連ブログ

マクローリン展開

(サイエンス)
【まくろーりんてんかい】

マクローリン展開
　関導数y=f(x) の関数y^'=f^'(x) の導関数を2階導関数といい、f^''(x),\frac{d^2}{dx^2}f(x),y^",\frac{d^2y}{dx^2}
と表す。さらに2階導関数の導関 3階導関数といい、f^'''(x),\frac{d^3}{dx^3}f(x),y^"',\frac{d^3y}{dx^3} 表す。一般にn-1 階導関数をn 階導関数とf^n(x),\frac{d^n}{dx^n}f(x),y^n,\frac{d^ny}{dx^n}いいと表すf^n(x) やy^n の表し方はn が大きいときも使う。
　高い階数の導関数を用いてテイラーの定理を呼ばれる次の定理を得られる[tex:a

マクローリン展開

(サイエンス)
【まくろーりんてんかい】

原点を中心としたテイラー展開。

リスト::数学関連

このタグの解説についてこの解説文は、すでに終了したサービス「はてなキーワード」内で有志のユーザーが作成・編集した内容に基づいています。その正確性や網羅性をはてなが保証するものではありません。問題のある記述を発見した場合には、お問い合わせフォームよりご連絡ください。
一浪理系大学生の奮闘記•6日前

テイラー展開！！

テイラー展開という言葉は多くの人が聞いたことがあるかもしれません。 しかし、どんなものなのかわからなかったり、どうやってつかうの？と疑問に思ったりする方も多いでしょう。 大学数学で最初に習うことになるテイラー展開。これは大学数学の入り口です。 なんか難しそう、いやだな、と感じるかもしれませんが一緒に学んでいきましょう。 目次 テイラー展開の定義 マクローリン展開の定義 テイラー展開ってなにしてるの？？？ テイラー展開の応用 終わりに テイラー展開の定義 区間[a, x]において、f(x)がｎ回微分可能であるとき、その区間に属する２点aとｘに対して、 と表すことが出来ます。この式をf(x)のx=…

#テイラー展開#数学#大学数学#マクローリン展開

ネットで話題

もっと見る
18ブックマークお前さあ、マクローリン展開って本来は大学レベルの話だよ？anond.hatelabo.jp
12ブックマーク高校生のための マクローリン展開（１）計算機（コンピュータや関数電卓）が無かった昔、人はどうやってsin, cos, tan の 値を求めていたのだろう？ （他にも 対数関数log や 指数関数exp なんていうのも値を求めるのが大変だ） まさか直角三角形の図を描いて長さを測定するなんてことはしていなかったと思う。 （自分でやってみると分かりますが、この方法は...chaosweb.complex.eng.hokudai.ac.jp
8ブックマーク高校生のための マクローリン展開（２）このコーナーに応援のメールを頂きました。ありがとうございます。 いやー、手を抜けなくなりましたなぁ ^^;。 前回は cos のマクローリン展開を示しました。 今回は他の関数のマクローリン展開を示し、その面白い利用方法を示しましょう。 実はマクローリン展開は単に計算に用いるだけではありません。新しい定理や公式...chaosweb.complex.eng.hokudai.ac.jp
6ブックマークテイラー展開とマクローリン展開（テイラー展開とマクローリン展開）　Taylor expansion　＆　Maclaurin's expansion　　2008.1.30 テイラー展開，マクローリン展開というものがあるが，高校数学では「ちら」っと触れるだけで， そこまで入り込む時間も，余裕も無いのが現実である。 更に言うと，「ちら」見が出来るのは，それなりの学力の高い学校で ...www.synapse.ne.jp
6ブックマーク世界で最も恐ろしい試験は「マクローリン展開の剰余項を求めよ。」 - Fallen Physicist, Rising Engineersci.tea-nifty.com
5ブックマークマクローリン展開無限回微分可能な関数 f( x ) について， f x =f 0 + f ′ 0 x+ f ″ 0 2! x 2 +⋯⋯+ f n 0 n! x n +⋯⋯ = ∑ n=0 ∞ f n 0 n! x n 参考：マクローリン定理 を f( x ) のマクローリン展開という ．これはテイラー展開において， a=0 としたものである． ■主な関数のマクローリン展開 1 1−x =1+x+ x 2 + x 3 + x 4 +⋯⋯+ x n +⋯ ...w3e.kanazawa-it.ac.jp
5ブックマークマクローリン展開 | 高校数学の美しい物語manabitimes.jp

関連ブログ

完全無欠で荒唐無稽な夢•3年前

マクローリン展開からの逸脱

x=0の近傍で微分可能な関数は下式に展開されるというのは高校で習った。 例えば、指数関数は となるが、 この分母を細工して、項を追加した場合はどんな関数（陽な表示）になるだろう？ 式の変形でこうなるのがわかる。 では、これはどうか？ 受験数学的だけれども、三角関数のバリエーションもある。 結果はこんな感じ。 三角関数の結果が代数的でないと陽表現にはならないだろう。 この関数のグラフだ。 ちょっとした変形なのに陽な結果がだせそうにないのが、これだ。分母の１がなければ、シンプルな分数式になる。 あるいは二項係数 Cを含む下式。 あるいは、手練な人ならなにかに結びつけることは可能かもしれない。 この…

#マクローリン展開#数学#級数
完全無欠で荒唐無稽な夢•4年前

ｅのx乗　指数関数の類似物件

指数関数eのx乗はx=0の近傍でのマクローリン展開するとこうなる。 つまり、 「!」は階乗の記号です。 ここでは、類似物のマクローリン展開式から構成される関数y(x)を見つけてみたい。 指数関数的にはなるだろう（後でグラフで比較してみる） 両辺をｘで微分すると微分方程式をえることができる。ガンマ関数の性質を使った。 ガンマ関数は階乗！の自然な拡張であります。 ベルヌーイ型の一階微分方程式なので、解析解が求められる。 結局の所、解の式はこうなった。案外、複雑になりますなあ。 この式ともとの級数和を重ね合わせると下のようになり、差異はないことがわかる。 おおもとの指数関数ｅ^xとの差異はどうなるだ…

#指数関数#微分方程式#マクローリン展開#数学#ガンマ関数#階乗