波動関数
(サイエンス)
【はどうかんすう】
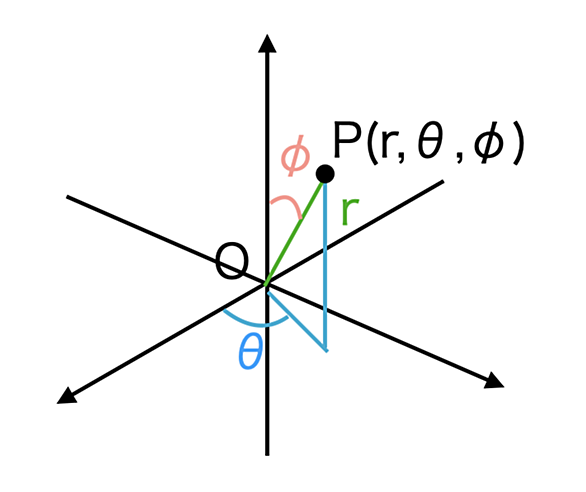
波動関数 (はどうかんすう、Wave function)は、もともとは波動現象一般をあらわす関数のことだが、現在ではほぼ量子状態(より正確には純粋状態)を表す複素数値関数のことを指す。
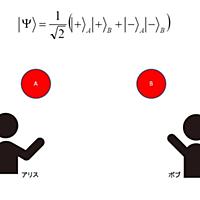
ブラケット記法においては、波動関数は状態ケットの位置固有状態への射影である。すなわち
物理的解釈
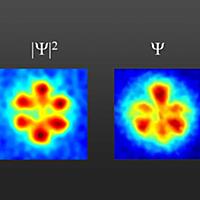
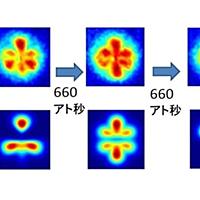
波動関数に物理的な解釈を与える。波動関数は位置
における確率振幅をあたえ、絶対値の2乗
は、位置
における微小体積
において粒子が見出される確率
を与えると解釈される。