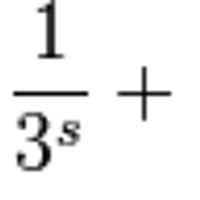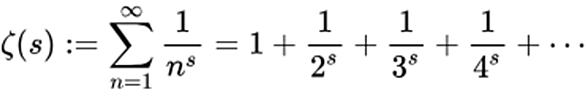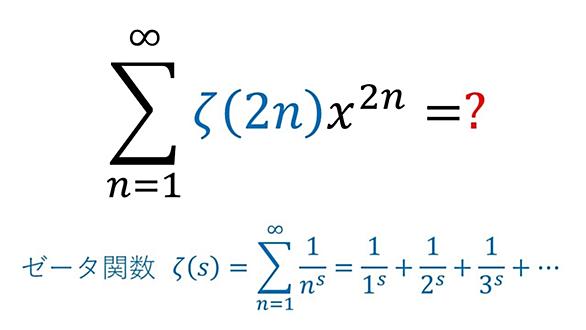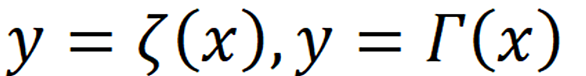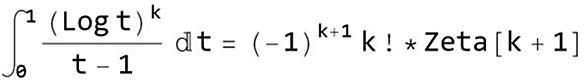ゼータ関数
(サイエンス)
【ぜーたかんすう】
以下のような関数.
素数の分布について多くの秘密を握っている。
例えばゼータの自然数nにおける値の逆数は
「n個の整数を勝手に取ったときそれらが互いに素になる」
確率に等しい。
歴史的にはオイラーが素数が無限に存在することの別証明のために考案し、後にリーマンが定義を拡張して複素解析的な扱いを試みた。
現在では、数学の対象で「素なるもの」の分布を探るためにゼータに似た関数がいくつか考案されていて、それらもゼータ関数と呼ばれる。例えばデデキントのゼータ関数、セルバーグのゼータ関数など。
*リスト:リスト::数学関連