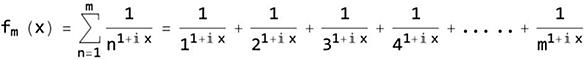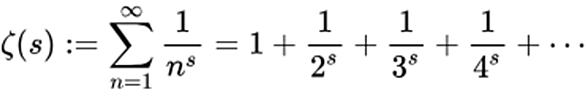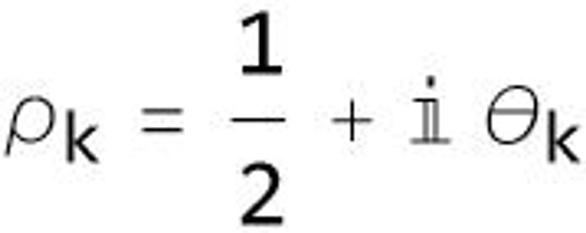リーマン予想

(サイエンス)

【りーまんよそう】

概要

リーマン予想 (Riemann Hypothesis, RH) は, ドイツのベルンハルト・リーマン (Bernhard Riemann, 1826 - 1866) が, 1859年に提出した論文『与えられた数以下の素数の個数について』 (Über die Anzahl der Primzahlen unter einer gegebenen Größe, 英訳 On the Number of Primes Less Than a Given Magnitude) で提唱した予想である. 素数の情報から生み出されたリーマンのゼータ関数の零点分布に関する予想である.

定式化

リーマン予想はよく「リーマンゼータ関数の零点の実部はすべて $\frac{1}{2}$ 」と定式化されているが, これはいくつかの点で明確な誤りを含んでいる. まず, リーマンのゼータ関数を以下のように定義する.

$\zeta(s) := \sum^{\infty}_{n=1}\frac{1}{n^s}$

この右辺の式は, 以下のように表せることが知られている.

$\zeta(s) = \sum^{\infty}_{n=1}\frac{1}{n^s} = \prod^{\infty}_{p:\r{prime}}\frac{1}{1-p^{-s}}$

自然数に渡る級数 (ディリクレ級数) とすべての素数にわたる積とが等しいという主張である.
この事実を示したのは18世紀最大にして最高の数学者と讃えられるスイスのオイラー (Leonhard Euler, 1707 - 1783) である. このことを記念して最右辺は「オイラー積」と呼ばれる. これは歴史的にも正しい呼称である.

オイラーが研究していた級数の定義域は実数全体であった. これを複素数全体に広げたのがリーマンの件の論文での仕事である.
定義域を広げるには「解析接続」というステップを辿る. 直感的には「ある領域で定義された関数と広げたい領域で定義された関数が実は等しいことを示す」という技法である. ゼータの場合, 実数で定義された表示と, 複素数全体で定義された「積分表示」とが等しいことを用いて示された.

このようなステップを経て, 解析接続されたゼータ関数の表示を見ると, 「自明な零点」の存在が分かる. リーマンゼータにおいて自明な零点とは「負の偶数」である. すなわち,

$\zeta(-2) = 0$
$\zeta(-4) = 0$
$\zeta(-6) = 0$
$\cdots$

ということである. 先ほど定義した級数や積の形からは想像しにくい値だが, 「解析接続後の表示を使っている」ことを常に意識せねばならない.

そして「複素関数」となったゼータに対し, 以下のようにリーマン予想を定式化する.

全複素平面上に解析接続されたリーマンのゼータ関数 $\zeta(s)$ の本質的 (非自明) 零点の実部はすべて $\frac{1}{2}$ である.

現在まで150年間多方面からアプローチされてきたが現在まで難攻不落な予想である.

リーマン予想と素数分布

ゼータ関数はオイラー積を見ると分かるように, 確かに素数の情報が含まれている. しかしリーマン予想はどの程度素数の本質にせまるものなのだろうか. 実はリーマン予想が真ならば, 「究極的な素数分布」が得られるのである. この辺りの事情は「素数定理」に関する理解が必要である.

素数定理とは, 1896年にド・ラ・ヴァレ・プーサンとアダマールによって独立に示された定理で, $x$ 以下の素数の個数を表す関数 $\pi(x)$ において,

$\lim_{x \rightarrow \infty} \frac{\pi(x)}{x/\log{x}} = 1$

という定理である. この証明を追うと, リーマンゼータの非自明零点が素数分布について本質的な鍵を握っていることが分かるのである.
素数はRSA暗号に代表されるように, 実用上極めて重要な概念であるが, リーマン予想によって究極的素数分布が判明すると, 日常生活にも大なり小なり影響を与えることとなりうるものなのである.