大数の法則
(サイエンス)
【たいすうのほうそく】
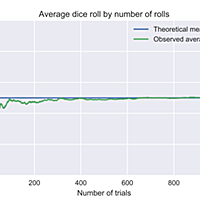
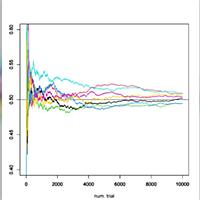
統計的確率(試行を繰り返して求めた確率)は、真の確率に近づくということ。
確率変数をX、Xの真の期待値をmとする。試行回数nが大きくなると
がmから遠くに離れる確率は小さい。(大数の弱法則)
がmに等しい。(大数の強法則)
弱法則と比べて、強法則は「確率」という言葉を使っていない点に注意されたい。強法則は、和をとっているだけである。
なお読み方は「たいすうのほうそく」であり、ある人が「だいすうのほうそく」と読んだ場合は例えば「大学への数学(略して大数)」の読者であった可能性がある。
→統計学関連、中心極限定理
大数の弱法則
- 確率変数
は全て独立。
の平均は全て
に等しい。
の分散は全て
以下である。
この時、以下が成立する。
大数の強法則
- 確率変数
は全て独立。
は全て同一分布に従う。
の平均は全て
に等しい。
この時、以下が成立する。
強法則では同一確率分布を前提としているが、弱法則は同一である必要はなく、分散が有界であることのみが必要である。