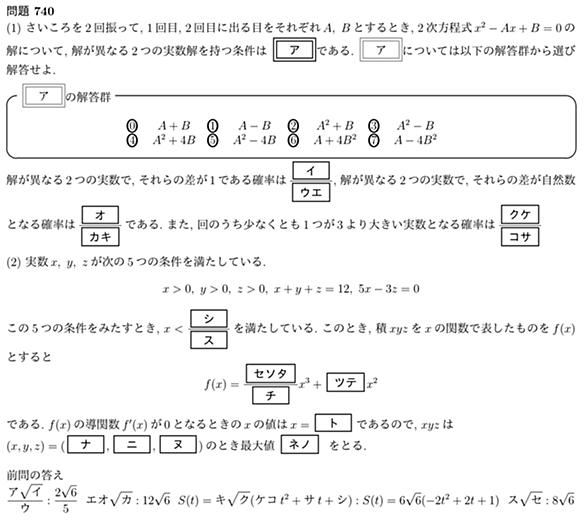
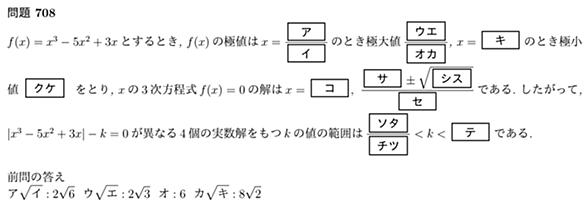
導関数
(サイエンス)
【どうかんすう】
ある関数 (微分可能であるとする) を微分することで新しく得られる関数．
もとの関数の増減を表す．すなわち，導関数が正である区間ではもとの関数は増加をつづけ，導関数が負である区間ではもとの関数は減少をする．導関数が 0 になる瞬間ではもとの関数の増加・減少が止まり，そこで極値をとる可能性がある．
*リスト::数学関連
このタグの解説について
この解説文は、すでに終了したサービス「はてなキーワード」内で有志のユーザーが作成・編集した内容に基づいています。その正確性や網羅性をはてなが保証するものではありません。問題のある記述を発見した場合には、お問い合わせフォームよりご連絡ください。関連ブログ
ネットで話題
もっと見る
www.anlyznews.com
www.mkamimura.com
www.mkamimura.com
www.geisya.or.jp
kou.benesse.co.jp
www.mkamimura.com
www.mkamimura.com
www.mkamimura.com6ブックマーク公式（微分）− 1 − 公式（微分） 導関数の定義 f′ (x) = lim h→0 f(x + h) − f(x) h = lim t→x f(t) − f(x) t − x 基本的関数の導関数 ( C )′ = 0 ( xα )′ = αxα−1 ( 1 x公式（微分）− 1 − 公式（微分） 導関数の定義 f′ (x) = lim h→0 f(x + h) − f(x) h = lim t→x f(t) − f(x) t − x 基本的関数の導関数 ( C )′ = 0 ( xα )′ = αxα−1 ( 1 xα )′ = − α xα+1 ( ex )′ = ex ( ax )′ = (log a)ax ( log x )′ = 1 x ( loga x )′ = 1 (log a)x ( sin x )′ = cos...
www.h6.dion.ne.jp
www.h6.dion.ne.jp
