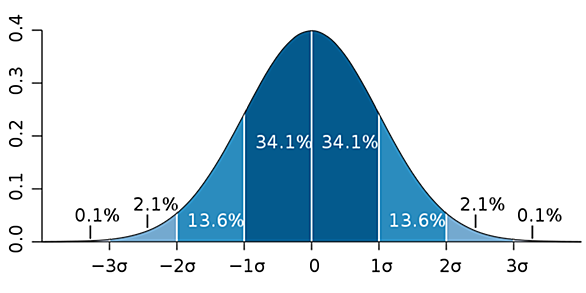
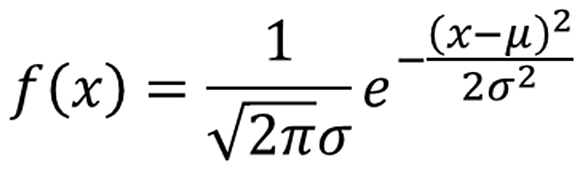正規分布
(サイエンス)
【せいきぶんぷ】
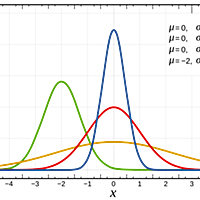
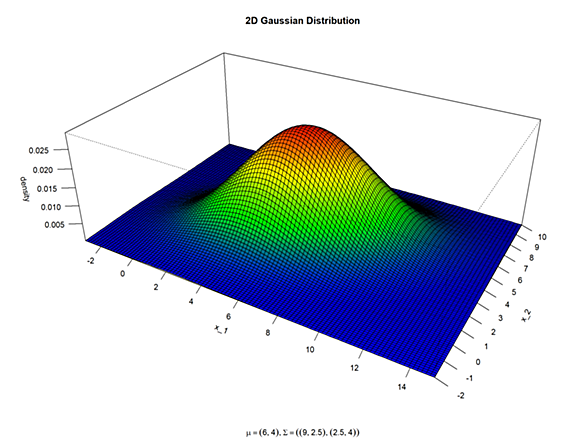
ガウス分布とも呼ばれ、次の式で表される確率密度関数を持つ確率分布。
ここで、は平均、
は分散であり、この正規分布を
と表す。
特に、かつ
のとき、標準正規分布と呼ばれる。
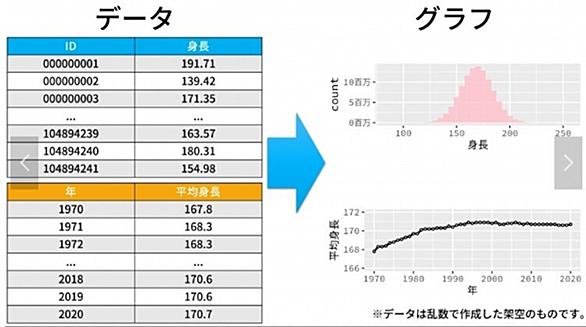
中心極限定理によれば、任意の確率分布に従う独立な変数を足し合わせた変数は、足す変数の数が多くなると正規分布に近付いていくことが知られている。何かを測定した場合の誤差は様々な独立な要因からくる変数の合計になっているので、正規分布に従うと考えられる(ガウスの誤差論)。
経済活動など、それに参加する多くの要素(人間)が互いに影響を及ぼしあっている場合はそれぞれの寄与が独立でなくなり、価格変動などが正規分布からずれる場合がある。
リスト::数学関連