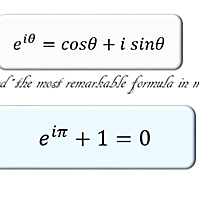オイラーの公式
(サイエンス)
【おいらーのこうしき】
[英] Euler's formula
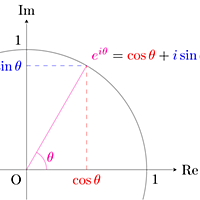
オイラーの公式とは、
で表される等式。ここでは2乗すると-1となる虚数単位、
はネイピア数である。
実数の世界では全くの無関係のように思われていた指数関数と三角関数が、複素数の世界では親戚どころか兄弟であったことを意味する重要な式であり、ファインマンはこれを「オイラーの宝石」と表現した。
証明はキーワード「テイラー展開」の「具体例」を参照。
オイラーの等式
この公式においてとすると、
あるいは
という「オイラーの等式」が導かれる。
この式は、
- ネイピア数
- 円周率
- 虚数単位
という、それまで全くバラバラの分野で扱われ、何の関係性も持ち得ないと思われていた3つの数が、実際には結び付けられるどころか、非常にシンプルな解を導き出すという非常に重要な等式である。
数学者たちはこの予想外の調和・連関を「人類の至宝」「人類史に残る不朽の名作」と表現している。
参照:[question:1105793000:title]
* リスト:リスト::数学関連
このタグの解説について
この解説文は、すでに終了したサービス「はてなキーワード」内で有志のユーザーが作成・編集した内容に基づいています。その正確性や網羅性をはてなが保証するものではありません。問題のある記述を発見した場合には、お問い合わせフォームよりご連絡ください。関連ブログ
ネットで話題
もっと見る関連ブログ
•2年前
オイラーの公式とフーリエ級数(ln(sinx))に関する数学の問題
ln(sinx)はフーリエ級数展開できることが知られている。(lnは自然対数) 過去に東北大学の院試験でそのことを証明する問題が出題された。 対称性やフーリエ級数展開の公式を使った誘導形式だったと記憶している。 このブログでは、オイラーの公式を使って証明したいと思う。 数学的には厳密ではないが、個人的には面白い証明を考えたので堪能していただけたら幸いです~^^ drive.google.com