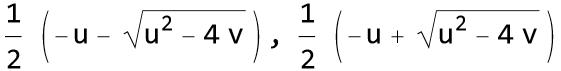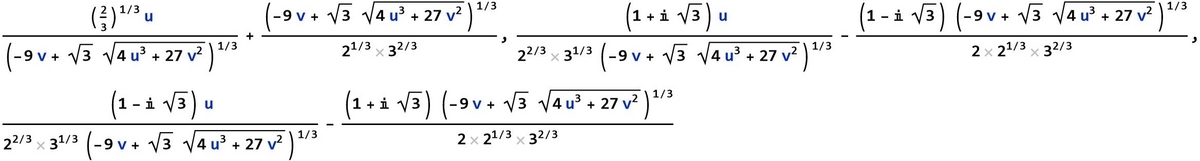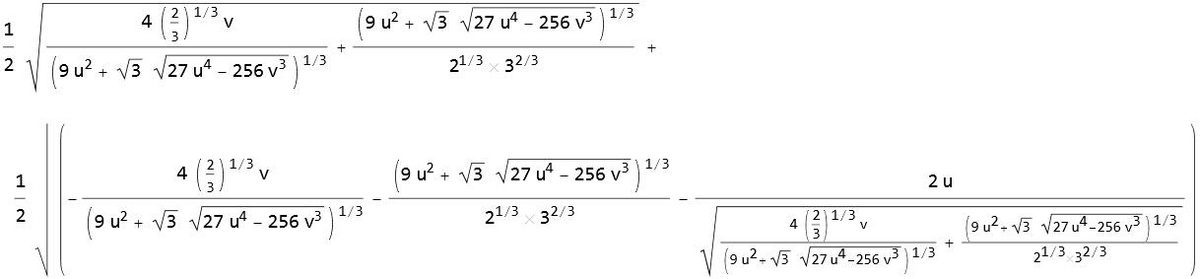手元に『ビジュアルリーマン予想入門』なる魅惑的な本がある。そのラストチャプターが「素数で輝く」なる瞠目の数値計算の章だ。
リーマン予想では下記のようなゼロ点集合ρが存在すると主張する。

Θはゼータ関数の解を与える実数である。これを使って、上記の本では関数Φを定義する。

この関数がを計算するとその頂点のx座標が素数とほとんど一致していることを示している。マンゴルトの公式の可視化というわけだ。
ある意味、素数というシンプルな数をゼータ関数のゼロ点の値という複雑な数から、再構成するわけである。
閑話休題。非力な自分が相手取るのは下式の数値の行方だ。nは自然数。

この極限の行き着く先がどうなるか。マンゴルトの式よりはシンプルだろう。
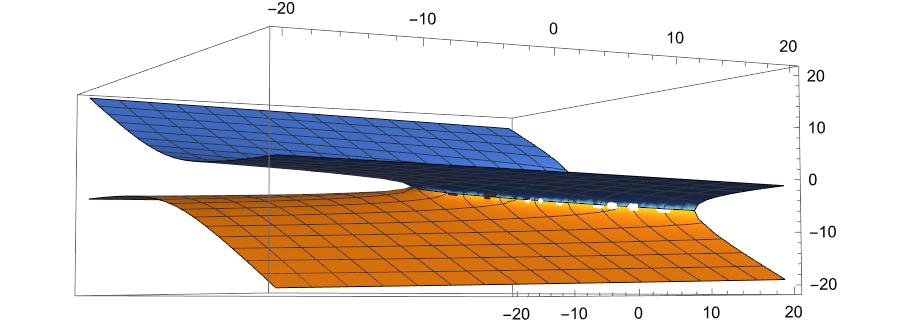
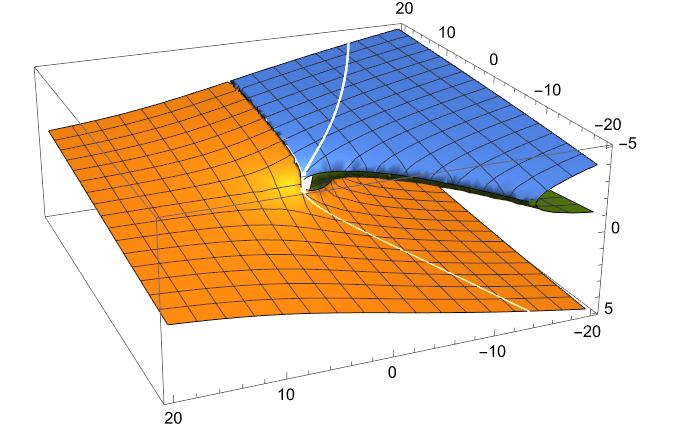
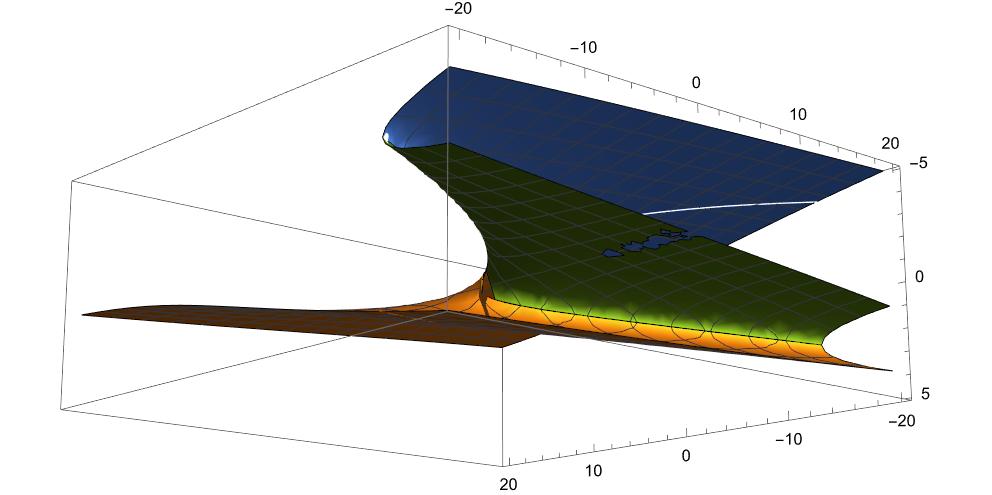
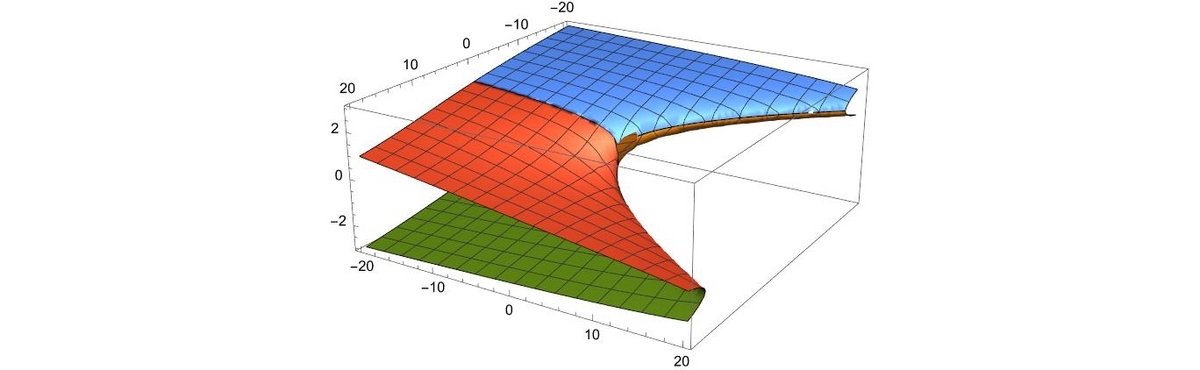
手はじめに、複素平面での初めの10000までの状況を示しておこう。
横軸は実数で縦軸は虚軸であるのは言うまでもない。虚数部は収束するようだ。
ちなみに、青い点は最初の40項の連続値。黄銅色の点は10,000までを250個サンプリングしている。

虚部についての数値計算の1000万までの結果を書き写しておこう。
1.78972411225932886
この数は愛読書の『数学定数事典』にはないようだ。
素数でも同じ操作を行っておこう。リーマン予想を冠した誹りを免れるためだ。
つまり、下の式の数値計算をするわけだ。Pnはn番目の素数だ。

虚部についての数値計算の初めの1000万個の素数までの結果を書き写しておこう。
0.778301336533066236
自然数のケースとほぼ「1」だけ違うのが興味深い。
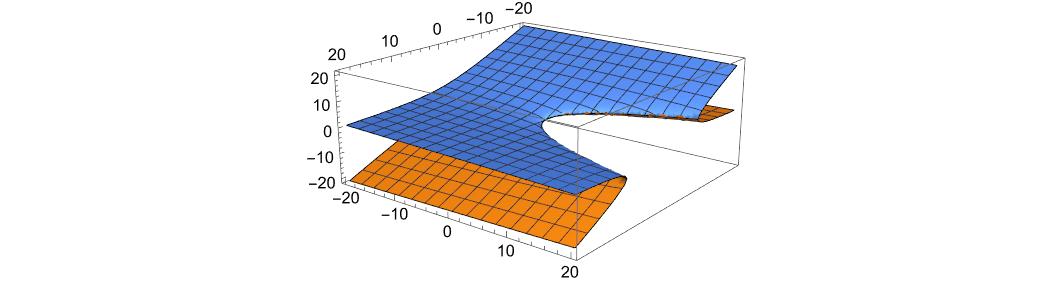
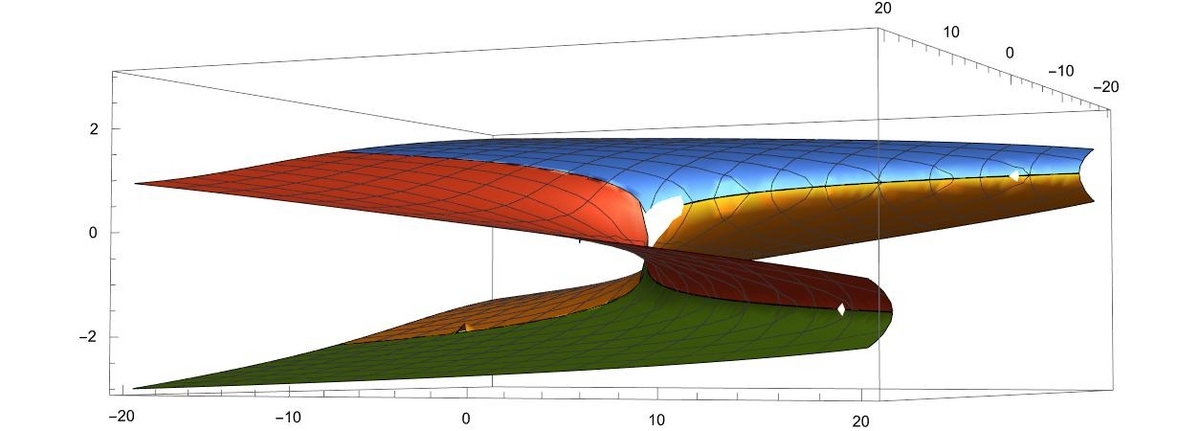
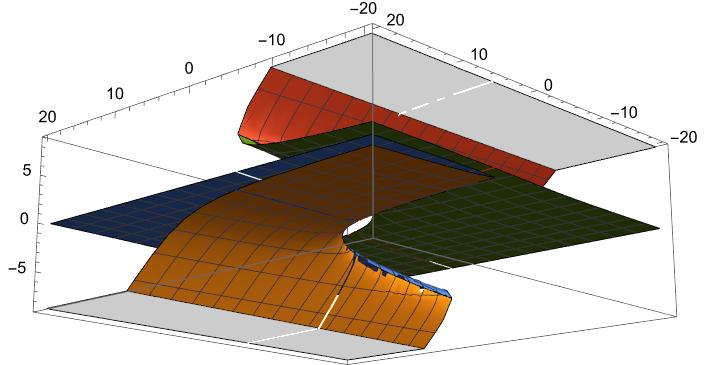
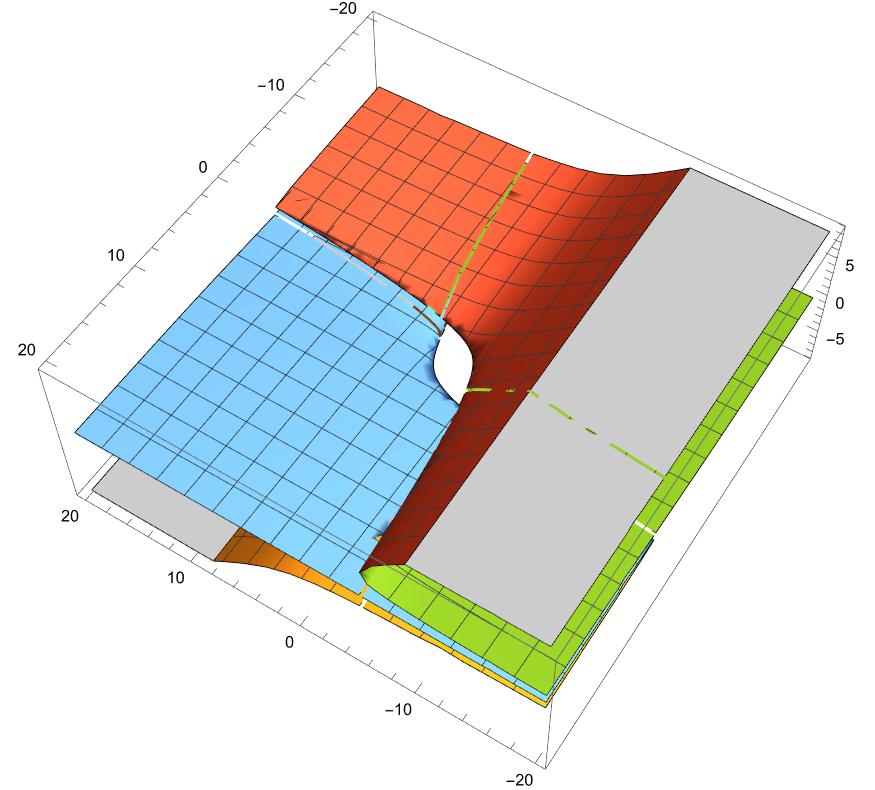
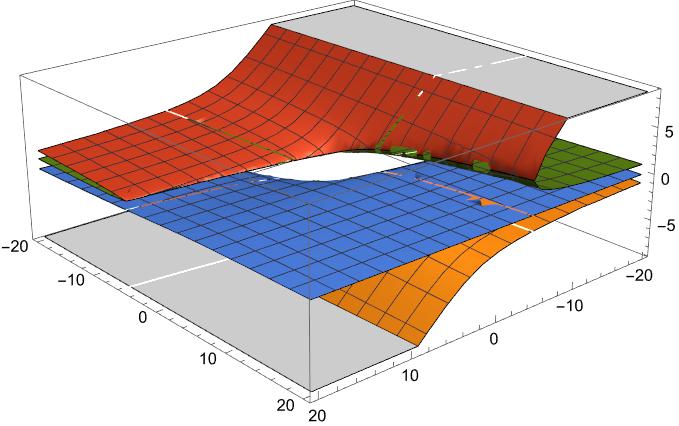
図示したものは下図となった。