運動方程式
(サイエンス)
【うんどうほうていしき】
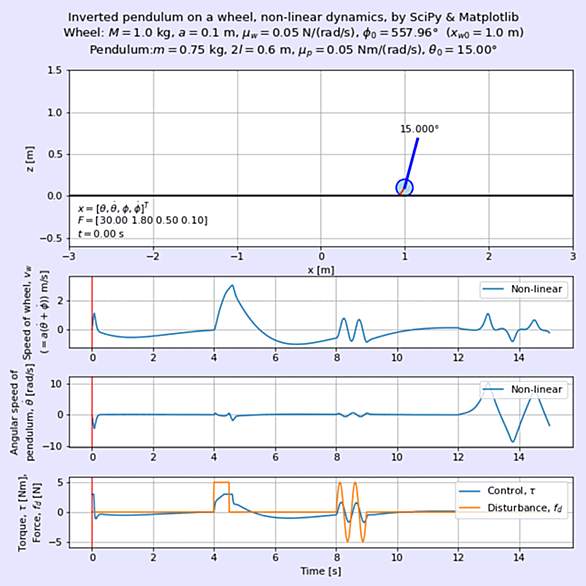
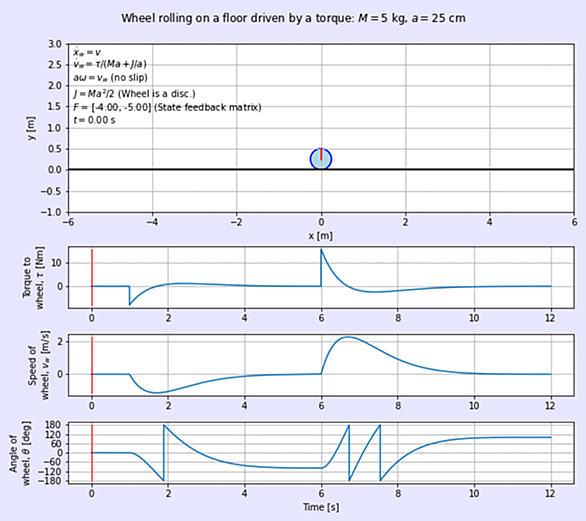
運動方程式とは、古典力学(ニュートン力学)の第二法則に当たる方程式で、運動量の時間変化と力が比例関係にあることを表した方程式のこと。
具体的には、質量を、加速度を
、力を
とおいたとき、
と表される式のことである。(高校物理での扱い)
この式を最初に発見し用いたのはアイザック・ニュートンであり、これはニュートンの三法則の第二法則となっている。
この式において、は位置
を時間
で二階微分したものであるから、以下のようにも表すことができる。(大学物理での扱い)